今天周日,准备读论文,论文是办公室同学小灿的。花了一天的时间,总算把论文读完了,果然我自己水平
还是太低了,只找到了10多个小的问题,而且语法问题一个也没有发现。果然读博士需要好的英语,但是我现在
的英语水平实在是不够用啊,有时间一定要好好学习英语!
今天,总结一下异常检测算法。
基于主成分分析的异常检测算法
该算法主要出自于论文:Control procedures for residuals associated with principal component analysis
算法原理
该方法详细介绍:
主成分分析首先将m行n列的数据矩阵A输入,中心化数据得到矩阵B,然后解得的特征值, 其中选择方差权重95%,使得
,
则得到值最高的k个特征向量。 将这些特征向量组成。因为主成分分析将高维的数据映射到低维空间中,使得每个高维数据到低维空间的距离之和达到最小, 因此大部分数据到低维空间中的距离比较小,所以该距离越大,可以认为原来的数据时间片更可能是异常时间段。 将最高的k个特征向量组成矩阵,则该矩阵的正交投影矩阵为。 因此如果原来的向量为y,则该向量到其映射的子空间的欧几里得距离通过计算平方预测误差(矢量的平方长度) 来形式化(其中是y到异常子空间上的投影,并且可以计算为,其中 由PCA算法选择的前个主成分组成。)
检测规则 :如果我们标记y是异常的如果: (其中表示在置信水平下SPE残差函数的阈值统计量。)
是样本数据协方差矩阵第j个主成分投影在子空间的特征值。 是标准正态分布的百分位数。
程序实现
根据这个公式,我们可以使用 中的主成分分析辅助完成这个操作,得到异常的Q值得代码如下:
def caculateQ_Alpha(df,pca,alpha):
#pca.fit(df)
r = pca.explained_variance_.size
pca = skldec.PCA()
pca.fit(df)
Phi_1 = 0
Phi_2 = 0
Phi_3 = 0
h_0 = 0
if r == pca.explained_variance_.size: #如果所有数据投影到原空间,则Q值都为零,该方法失效
return 0
for i in range(r,pca.explained_variance_.size):
Phi_1 = Phi_1 + pca.explained_variance_[i]**1
Phi_2 = Phi_2 + pca.explained_variance_[i]**2
Phi_3 = Phi_3 + pca.explained_variance_[i]**3
# print(str(Phi_1)+'\t'+str(Phi_2)+'\t'+str(Phi_3))
h_0 = 1 - 2*Phi_1*Phi_3/(3*Phi_2**2)
C_alpha = norm.cdf(alpha) #得到正态分布alpha的百分位数
delta2_Alpha = Phi_1*(C_alpha*math.sqrt(2*Phi_2*h_0**2)/Phi_1 + 1 +
Phi_2*h_0*(h_0-1)/Phi_1**2)**(1/h_0)
return delta2_Alpha
然后可以将读取数据使用这个Q值的方法的过程计算出来,得到异常的数据行数,并且将所有数据的Q值画出来
,这样就能直观的看的Q异常所在的对于异常数据点。对于异常,我们也可以分下类,对于小于给定阈值的数据
当做正常Normal,然后大于阈值,小于两倍阈值的为轻微点的异常Slight,往下继续分为Warning、error
和Critical
该实现代码如下:
def caculateLogVector(fileName):
# 读取数据
df = pd.read_excel(fileName)
pca = skldec.PCA(n_components = 0.90)
pca.fit(df) #主城分析时每一行是一个输入数据
result = pca.transform(df)
df_origin = pca.inverse_transform(result)
ndarr = np.array(df) #输入数据,这里每一行是一个输入数据
ndarr = preprocessing.scale(ndarr,with_std=False) #中心化数据
Y = ndarr.T #使得每一个列是一个输入数据
#result2 = pca.components_.dot(Y).T #该结果等于使用pca的transform的结果
P = pca.components_.T #原来公式里的P是主成分列向量组成的
Y_a = Y - P.dot(P.T).dot(Y)
Y_a_2norm_sqr = np.zeros(Y_a.shape[1]).reshape(1,Y_a.shape[1])
for i in range(Y_a.shape[1]):
Y_a_2norm_sqr[0,i] = np.linalg.norm(Y_a[:,i])**2
#sns.distplot(Y_a_2norm_sqr);
#sns.tsplot(data=Y_a_2norm_sqr[0,:10000],err_style = "ci_bars",interpolate = False)
x = np.linspace(1, Y_a.shape[1] , Y_a.shape[1])
plt.scatter(x,Y_a_2norm_sqr, s=2)
plt.xlabel(u'Sample Datas',{'color':'r'})
plt.ylabel(u'Q Values',{'color':'r'})
#plt.hold
lineToDraw = caculateQ_Alpha(df,pca,0.05)
plt.plot(x,[lineToDraw for i in range(Y_a.shape[1])],'-r',label = 'normal',linewidth=1)
plt.plot(x,[2*lineToDraw for i in range(Y_a.shape[1])],'-g',label = 'slight',linewidth=1)
plt.plot(x,[4*lineToDraw for i in range(Y_a.shape[1])],'-b',label = 'warning',linewidth=1)
plt.plot(x,[8*lineToDraw for i in range(Y_a.shape[1])],'-k',label = 'critical',linewidth=1)
plt.legend()
# return 异常对应的序号
#==============================================================================
# numListToReturn = {'Critical':[],
# 'Error':[],
# 'Warning':[],
# 'Slight':[],
# 'Normal':[]};
# for i in range(Y_a_2norm_sqr.shape[1]):
# if Y_a_2norm_sqr[0,i] > 8*lineToDraw:
# numListToReturn['Critical'].append((i,Y_a_2norm_sqr[0,i]))
# elif Y_a_2norm_sqr[0,i] <= 8*lineToDraw and Y_a_2norm_sqr[0,i] > 4*lineToDraw:
# numListToReturn['Error'].append((i,Y_a_2norm_sqr[0,i]))
# elif Y_a_2norm_sqr[0,i] <= 4*lineToDraw and Y_a_2norm_sqr[0,i] > 2*lineToDraw:
# numListToReturn['Warning'].append((i,Y_a_2norm_sqr[0,i]))
# elif Y_a_2norm_sqr[0,i] <= 2*lineToDraw and Y_a_2norm_sqr[0,i] > 1*lineToDraw:
# numListToReturn['Slight'].append((i,Y_a_2norm_sqr[0,i]))
# else:
# numListToReturn['Normal'].append((i,Y_a_2norm_sqr[0,i]))
#==============================================================================
numListToReturn = {'Abnormal':[],
'Normal':[]};
for i in range(Y_a_2norm_sqr.shape[1]):
if Y_a_2norm_sqr[0,i] > lineToDraw:
numListToReturn['Abnormal'].append((i,Y_a_2norm_sqr[0,i]))
else:
numListToReturn['Normal'].append((i,Y_a_2norm_sqr[0,i]))
return numListToReturn,df
调用该函数的代码如下:
import matplotlib.pyplot as plt #用于类似matlab绘图的包
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
from sklearn import decomposition as skldec #用于主成分分析降维的包
from mpl_toolkits.mplot3d import Axes3D #用于3D绘图的包
import seaborn as sns #用于高阶画图的包
import pandas as pd
import numpy as np
from sklearn import preprocessing #用于预处理的包
import math #用于计算开方
from scipy.stats import norm #用于计算标准正态分布的分位数
if __name__ == '__main__':
FileName = "test.xlsx"
# drawTypeCorrlation(FileName)
[AnomalousLine,df] = caculateLogVector(FileName)
这样就可以得到异常数据的图片:

根据该图片,即可看到异常数据大致出现在哪。
绘制相关统计图
为了观察异常和正常的属性之间的差别,我们可以使用Seaborn相关的工具函数进行绘制,代码如下:
def generateDrawDF(strList,df,AnomalousLine): #得到可以进行绘画的数据
data = [];
for i in range(len(strList)):
levelList = AnomalousLine[strList[i]] #得到等级对应的列表
for j in range(len(levelList)):
lineNum = levelList[j][0] #得到行号
LineSeries = df.iloc[lineNum] #得到行的序列
for k in range(int(LineSeries.size)):
#print(LineSeries[k],LineSeries.index[k],strList[i])
data.append((LineSeries[k],LineSeries.index[k],strList[i]))
#下面一行绝对不要用,DataFrame绝对不要动态加行列!!!!
# Drawdf.loc[Drawdf.iloc[:,0].size] = [LineSeries[k],LineSeries.index[k],strList[i]]
# print('计算了一次')
# print(data)
Drawdf = pd.DataFrame(columns=('times','type','level'),data = data)
return Drawdf
if __name__ == '__main__':
FileName = "test.xlsx"
# drawTypeCorrlation(FileName)
[AnomalousLine,df] = caculateLogVector(FileName)
strList = ['Normal','Abnormal']
Drawdf = generateDrawDF(strList,df,AnomalousLine)
plt.figure()
sns.boxplot(x="type", y="times", hue="level",
data=Drawdf, palette="Set2")
plt.figure()
result = sns.barplot(x="type", y="times", hue="level", ci = None , capsize=.1, #errwidth = 0,
data=Drawdf, palette="Set2")
plt.figure()
sns.violinplot(x="type", y="times", hue="level",
data=Drawdf, palette="Set2")
这样得到的图像如下:


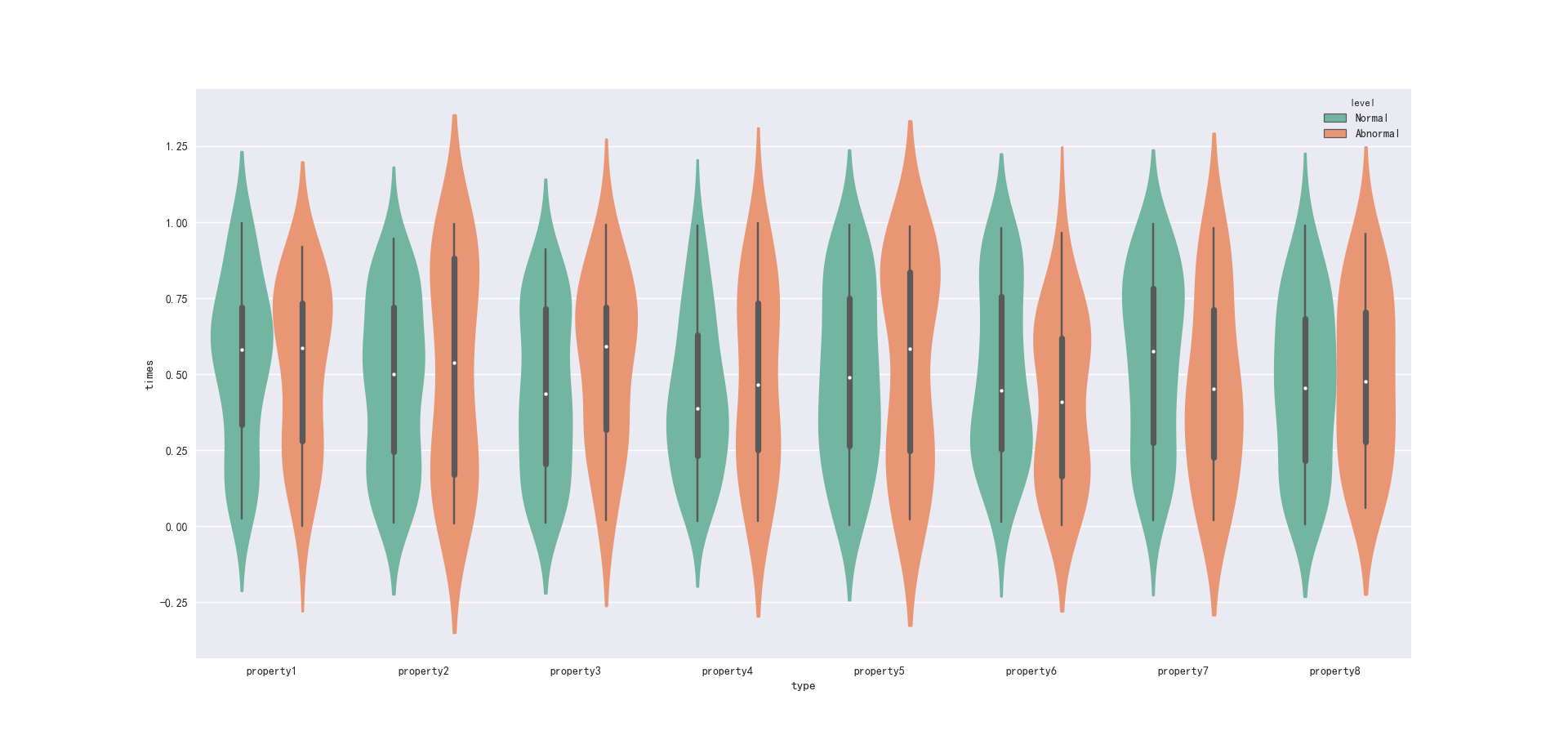
最后,本篇的全部代码在下面这个网页可以下载:
https://github.com/Dongzhixiao/Python_Exercise/tree/master/deviationDetection_PCA