回到主页

目录

• 目录
• Online System Problem Detection by Mining Patterns of Console Logs
  • Abstract:
    • 1. INTRODUCTION(介绍)
    • 2. RELATED WORK(相关工作)
    • 3. CONSOLE LOG PREPROCESSING(控制台日志预处理)
    • 4. TWO-STAGE ONLINE ANOMALY DETECTION(两阶段在线异常检测)
    • 5. STAGE 1: FREQUENT PATTERN MINING(阶段一：频繁模式挖掘)
      • 5.1 A. Combining time and sequence information(A.结合时间和序列信息)
      • 5.2 B. Estimating distributions of session durations(B.估计会话持续时间的分布)
      • 5.3 C. Implementation of Stage 1(C.阶段一的实现)
    • 6. STAGE 2: PCA DETECTION(阶段二：PCA检测)
    • 7. EVALUATION(评价)
      • 7.1 A. Stage 1 Pattern mining results(A.阶段1模式挖掘结果)
      • 7.2 B. Detection precision and recall(B.检测精度和召回率)
      • 7.3 C. Detection latency(c.检测延迟)
      • 7.4 D. Comparison to offline results(D.与离线结果比较)
    • 8. DISCUSSION(讨论)
    • 9. CONCLUSIONS AND FUTURE WORK(结论，未来工作)
    • 10. REFERENCES(参考文献)
    • 11. 附录
      • 11.1 分类算法的评估方法

Online System Problem Detection by Mining Patterns of Console Logs

Abstract:

• 本文描述了一种新的应用方式：使用数据挖掘和统计学习方法，在线自动跟踪控制台日志并检测异常
• 与现有的解决方案不同，作者采用了两阶段检测系统
  • 第一阶段使用频繁模式挖掘和分布估计技术来捕获主导模式(包括频繁序列和持续时间)
  • 第二阶段利用基于主成分分析的异常检测技术识别实际问题
• 使用来自一个203节点Hadoop[1]集群产生的真实系统数据，展示了
  • 不仅可以实现高度准确和快速的问题检测
  • 还可以帮助操作者更好地理解他们系统中的执行模式

1. INTRODUCTION(介绍)

【被忽略的控制台日志】

如今，互联网服务通常在由数千台服务器组成的数据中心中运行。在这些级别中，非故障停止性能故障很常见，甚至可能预示着严重的即将发生的故障。因此，运营商希望尽快得到此类问题的通知。尽管存在各种监视工具，但是每个应用程序中已经可用的监视常常被忽略:简陋的控制台日志。

【在线控制台日志分析很难】

控制台日志的作者和实际操作人员不同，内容不友好，不利于分析，更别提在线分析了！

【前文离线分析检测很有有意义，而后本文是描述如何是在线工作】

作者之前的工作在将统计机器学习和信息检索应用于控制台日志分析[28]问题上显示了良好的前景。具体来说，源代码分析从控制台日志恢复结构，异常检测技术推断哪些消息集可能指示操作问题。然而，那篇文章的工作是一种离线算法，该算法检查一个多天操作会话的整个日志，而操作人员需要了解这些问题的发生。

【本文第一个贡献】

• 一种新的两阶段在线日志处理方法，它将频繁模式挖掘与基于主成分分析(PCA)的异常检测相结合，用于系统运行时问题的检测
• 展示了如何通过使用时间戳信息增加频率序列信息来权衡在线设置中的时间检测和准确性。方法是完全自动的，不需要有使用的机器学习技术的专门知识也可以调整输入参数
• 本文方法是通用的：[28]调查了22个系统，其中大多数系统的日志都符合本文描述的方法。本文方法的模式挖掘方面可以帮助操作者即更好地理解系统行为（即使是在系统正常的情况下）

【本文第二个贡献】

在[28]中使用的相同标记数据集上对本文的技术进行实证评估：
在一个203台机器集群上使用开源应用程序Hadoop File System (HDFS)[1]运行48小时中，产生的2400万行自由文本日志。本文成功地识别了业务问题的异常情况；几乎在所有评价方面，都匹配或超过了离线方法的检测精度，检测延迟较小。 说明本文方法适合在线使用！

【本文的其余部分章节安排】

• 在第二节中，回顾了相关工作
• 第三部分回顾离线的方法[28]中的一些内容，这些方法同时也使用在的线上方法中使用
• 在第四节中详细介绍线上方法
• 第七节中将展示实验结果并评价本文方法的局限性和其他值得注意的方面
• 第八部分展示结果
• 在第九节结尾

2. RELATED WORK(相关工作)

【在线日志分析】

• [20,8,18]使用人工编辑规则(正则表达式等匹配日志)，软件更新时则需要维护规则从新人工编辑。而本文“自动”发现规则。
• Sisyphus[23]提供了一些在线分析方法，这些方法基于不同组日志的相关率(relative ratio)，为了抵消日志们的随机交错，必须聚集长时间的日志(数十分钟)
• [9,17]使用时间序列分析技术来建模周期事件的时间间隔。这些模式模拟事件周期性的长期趋势，而本文监控单个事件的跟踪。

【基于路径的分析(Path-based analysis)】

• Chen, Kıcıman et al.使用聚类[2]和概率上下文无关文法(probabilistic context free grammars)[3]来通过手工结构化软件部件在服务器系统中分析执行路径
• X-Trace[6]现在为跨分布式系统的基于路径的跨层仪器收集提供了一个框架

本文从控制台日志收集跟踪信息，而不是检测应用程序，因此本文必须处理噪声跟多的数据，而不是由检测产生的数据，本文的分析技术也适用于路径数据

【利用数据挖掘技术解决计算机系统问题】

在频繁模式挖掘[7]这一活跃的研究领域中，我们对序列模式挖掘技术尤为感兴趣，它将频繁发生的有序子序列作为模式进行挖掘

• 广义序列模式(GSP)[22]是一种基于先验的算法具有代表性的工作
• SPADE[31]是一种垂直的基于格式的挖掘方法
• PrefixSpan[19]是一种用于顺序模式挖掘的模式增长方法

本文扩展了这些技术，以解决在第五节中描述的独特问题的挑战

• 频繁模式挖掘技术还在分析消息中的单词中使用，以了解控制台日志[24]、[25]的结构，并发现Linux内核[14]中重复出现的运行时执行模式

本文的频繁模式分析侧重于异常检测

• 数据挖掘已广泛应用于端主机和网络[27]、[12]、异常事件检测等入侵[13]、[30]、检测系统和软件bug[15]、[32]以及配置问题[26]。这些技术在我们使用单个操作的跟踪时分析聚合数据。
• [23]使用信息论来查找日志中最可能表示实际问题的单词。相反，我们考虑消息跟踪并检测这些跟踪的异常
• [29]使用来自原始日志跟踪的隐藏Markov模型(HMMs)的混合来建模序列模式。由于日志消息的交错特性，该模型非常复杂

3. CONSOLE LOG PREPROCESSING(控制台日志预处理)

本小节回顾了能用于本文中的线上方法，必要的预处理如下：

• 解析日志以恢复日志消息中的固有结构
• 通过自动发现与同一程序对象(数据块、文件名等)相关的消息，并将其按顺序排列，重构踪迹(相关事件的执行序列)
• 从踪迹中构建数值特征向量从而进行基于PCA的分析

【日志解析】

• 通过源码分析可以以很高的精度找到日志模式——消息类型和消息变量
• 按照[9]中的系统管理工作，作者使用术语 event 来指代包含已解析日志消息元素的数据结构，本文中使用 tuple 处理每条消息———(时间戳,消息类型,[消息变量列表])。在线系统中，控制台日志流经过处理后变成了事件流

【确定事件踪迹】

本文的检测技术依赖于分析踪迹，踪迹是与同一程序对象相关的事件集

例如，一组引用同一文件的打开、定位、写入和关闭的消息将构成该文件的事件踪迹

然而，在事件流中，不同类型和引用不同变量集的事件都是交错的。从流中提取踪迹的一种方法是按事件的特定字段分组，这是流数据处理的典型操作
——问题是如何自动确定分组？

• 本文使用[28]中描述的方法，该方法通过发现哪些消息变量对应于程序操作的对象的标识符，自动从历史日志数据中找到分组。所有相同标识符的事件构成该标识符的事件踪迹。这种分组也在流处理器中使用。通过事件分组，本文实现了一个简单的分组流处理器，它将单个交错事件流转换为多个事件跟踪，每个跟踪对应一个标识符。特别是，假设事件踪迹彼此独立

【表示事件踪迹】

• 需要将事件跟踪转换为适合于应用PCA检测器的数字表示（本文方法的第二阶段）
• 在[28]中，每个完整的事件跟踪由消息计数向量(message count vector，MCV) 表示，它的结构类似于信息检索中的词袋模型，其中文档是事件跟踪中的一组消息，其中
  • $N$代表消息类型数
  • 向量元素$y_i$的值为事件$i$在一组中出现的次数(对应于“词频”)

消息数向量是事件踪迹的压缩表达，但是在线上场景中使用该方法时存在有两个问题：

• 首先，它们不携带任何时间信息，因此它们不能用于检测由于时间间隔太大(即速度太慢)而异常的操作
• 其次，原始的消息数向量是基于可以跨越任意长时间的整个事件跟踪来构造的，在线环境中通常是不可用的

本文使用消息数向量来表示会话，我们将会话定义为表示系统中单个逻辑操作的事件踪迹中的一个子集事件，并且预测的持续时间来进行限制。第四节中展示如何自动发现会话

4. TWO-STAGE ONLINE ANOMALY DETECTION(两阶段在线异常检测)

• 与[28]等离线方法相比，在线分析的基本问题是我们不能一次看到完整的事件跟踪
  举例子——在脱机检测中，由于缺少事件，跟踪可能被标记为异常：

  例如，如果对文件的写操作失败，它的跟踪可能缺少关闭消息。在在线分析中，没有办法知道(除了等待运行结束)丢失的事件是否会出现，但是在线检测的全部要点是及时做出评估。在此强调检测时间只取决于算法需要等待多长时间才能做出决定。与此等待相比，检测算法的计算时间可以忽略不计

• 因此，有效的在线检测需要在准确性和检测时间之间取得平衡。

  试想这样的极端情况下，如果我们在尝试在任何检测之前等待看到整个跟踪，那么我们的结果应该与脱机检测一样准确，但是需要花费大量的时间进行检测。在另一个极端,如果我们试图一旦出现单个事件就进行异常检测，我们就失去基于模式(一组相关的事件)来执行异常检测的能力。然而[28]表明，分析模式，而不是分析个别事件是准确检测的关键。

本文通过设计一种两阶段检测方法来权衡这个问题：

• 第一阶段使用频繁模式挖掘来捕获最常见的（比如：正常的）会话，即那些具有高支持度的踪迹。模式包括频率事件集和时间信息。此信息可用于确定踪迹何时 “可能完成”，并可用于异常检测
• 第二阶段只考虑通过第一阶段过滤后的的非模式事件，将基于PCA的异常检测应用到这些事件。在每个阶段，我们都基于文件历史数据构建一个模型，并定期用新的数据对其进行更新，并将其用于在线检测。模型估计和在线检测都涉及到对控制台日志的特定领域的考虑

图2清楚地显示了为什么需要两阶段方法:

• 从我们数据中不同事件轨迹的直方图可以看出，有些踪迹非常频繁，而有些踪迹则非常罕见

• 将主要踪迹标记为正常行为，将罕见的踪迹标记为异常，是很合理的

• 但这留下了大量既不明显正常也不明显异常的中间地带。这些位于中间地带的踪迹有时是带有随机噪声的正常痕迹，如交错痕迹。

• 本文希望检测方法能够容忍随机噪声

  如果我们减少最小支持级别以包含更多这些中间情况，则模式将引入随机噪声(例如重叠或不正确的排序)，从而降低模式的质量。

  • 本文将中间情况作为非模式事件传递给基于PCA的异常检测器

    由于PCA是一种能够匹配不精确模式的统计方法，因此它对随机噪声的鲁棒性比第一阶段使用的频繁模式挖掘更强，能够检测到中间情况下的罕见事件。直观地说：

    • （1）基于模式的方法对大多数事件提供了及时的检测，最小化了等待完整跟踪的时间
    • （2）而后续基于PCA的检测则处理了第一阶段产生的错误警报，大大提高了检测的准确性

• 两阶段方法的另一个好处是，阶段1中的频繁模式可以帮助操作人员更好地理解其系统的行为，并优化检测以包含特定于领域的知识

解释频繁模式和PCA结合的好处：

• 与模式挖掘相比，PCA对随机噪声的鲁棒性更强，是一种适合于处理有噪声的中间事件的方法
• 但频繁模式挖掘的优点是能够捕获事件之间的时间信息，并能直观地表示出主要模式
• 作者的两阶段方法综合了这两种方法的优点

下面详细描述每个阶段

5. STAGE 1: FREQUENT PATTERN MINING(阶段一：频繁模式挖掘)

正如第3节中定义的，事件踪迹是报告相同标识符的一组事件。进一步定义：

• 将会话定义为同一事件踪迹中具有可预测持续时间的密切相关事件的子集
• 会话的持续时间是会话中事件的最早时间戳和最新的时间戳之间的时间差

作者将定义频繁模式的会话及其持续时间分布特点:

• 1)会话在多个事件踪迹中频繁出现
• 2)大部分(例如99.95%)会话持续时间小于$T_{max}$, $T_{max}$是用户指定的最大允许检测延迟(事件发生到决定该事件是正常还是异常之间的时间)。

条件(1)保证模式覆盖普通情况，因此它可能是一种正常行为。条件(2)保证在短时间内检测到模式。我们定期挖掘归档数据以寻找频繁模式。这些模式用于过滤在线阶段中的正常事件。

我们不能应用一般的频繁序列挖掘技术，因为：

• 1)会话在事件跟踪中有许多交错(例如，两次读取同时发生)，因此事务边界不清楚。我们需要同时进行事件踪迹分割成会话和模式挖掘。然而，由于会话的持续时间可能有很大的变化，固定的时间窗口不能提供令人满意的分割，这就意味着我们需要对持续时间的分布进行建模
• 2)在分布式系统中，由于时钟不同步，事件在跟踪中可以被重新排序，这就预示着需要对事件使用总排序的技术。

  下面描述的算法中，使用频繁模式可以容忍随机会话交错导致的基于时间的分割精度较低的问题。一旦发现频繁模式，就可以使用它来解交错事件，以估计一个准确持续时间模型

5.1 A. Combining time and sequence information(A.结合时间和序列信息)

本文新方法结合了时间和事件序列信息，采用三步迭代的方法进行准确的模式检测。简而言之：

• 首先使用时间信息(不准确地)将事件踪迹分割为会话，然后挖掘这些不准确的片段来识别最常见的模式
• 然后回到原始数据找出实际会话时间分布最频繁的模式
• 最后从原始数据中删除与此频繁模式匹配的所有事件，并对其余数据进行迭代，以找到下一个最频繁的模式

1.使用时间间隔在每个执行跟踪中查找第一个会话（粗略的）
在这一步中，对于每个执行的追踪程序，我们首先扫描每个事件，直到找到这样一个事件， 其后一个事件的时间间隔长度是执行序列开始以来持续时间的10倍以上(时间间隔大小是一个可配置参数)。 我们将该间隔之前的所有事件视为一个会话(由MCV表示)。

这种分割可能非常不准确：由于会话的交错，可能会在会话中包含不相关的事件，并且由于会话持续时间的随机性，可能会在会话中丢失事件。在下一步发现频繁模式时，可以容忍这种不准确性

2.识别显著会话
这里提出一种在一个会话中包含所有事件的模式。在真实环境的大多数情况下，由于会话的分段方式：发生在很短的时间内的会话有高概率(虽然不总是)表明该会话代表一个单一的逻辑操作，特别是当支持度很高的情况下

我们使用两个标准来选择显著的模式：

• (1)我们从所考虑的所有会话的 medoid 开始(回想一下，会话已经由MCVs表示)。根据定义， medoid 与所有其他数据点的聚合距离最小，这表明它是所有数据点的良好代表。直观地说，medoid 类似于空间中的质心(或平均值)，只是 medoid 必须是实际的数据点

  标准(1)保证所选的主要会话是所审查会话的良好代表

• (2)我们要求从所有$M$个事件踪迹中得到的会话数目的最小支持度为$0.2M$。如果 medoid 不满足此最小支持度，则选择满足此最小支持的下一个最近的会话(数据点)

  标准(2)除了是一个适合的代表之外，还保证所选的会话实际上占主导地位。选择标准在很大范围的最小支持值上是稳定的，因为正常的踪迹在日志中占大多数【我认为这句话说明平均几何中心受到频繁模式影响较大】。事实上，在我们的实验中，$0.1M$到$0.5M$之间的各种支持值都得到了相同的选择结果

我理解的是因为一个踪迹包含多个会话，所以可以按照1，找出每个踪迹的所有会话(预处理阶段，所以不用管$T_{max}$)，然后按照2计算所有会话MCV的几何中心点，然后找到距离最近并且满足支持度大于$0.2M$的会话当做频繁(模式/会话)，这也承接上文说明了这里“不能应用一般的频繁序列挖掘技术”

3.使用频繁会话细化结果并计算持续时间统计信息
步骤2中的模式基于粗分段的会话，并且可能不能反映该类型的所有会话的正确持续时间分布：

• 因此返回原始数据，找到与频繁会话匹配(注：这里的匹配我开始理解仅仅是数量上的匹配，后来感觉是序列上的匹配)的所有事件

• 然后从匹配会话中估计持续时间分布(详细信息见第5节的B小节)

  使用持续时间分布,可以计算截止时间$T_{cut}$(该变量这里第一次出现，代表大多数会话模式应该完成的时间)模式$η^{th}$百分位的分布。在第7节的B小节中表明，这一步显著改善了检测结果

• 我们还从原始跟踪中删除所有匹配的事件，为下一次迭代准备数据。请注意，$T_{cut}$可能非常长，这是由于某些操作中的持续时间差异很大。在$T_{cut} > T_{max}$的情况下，该频繁模式被丢弃，在检测阶段不使用。(注：根据这句话我推测本文的方法包含检测阶段和预处理阶段！)

• 然后，我们返回到步骤1并进行迭代，直到没有保留最低支持度的模式。

  因为步骤3总是从数据集中删除一些东西，所以迭代一定会终止。 其余事件用于构建PCA模型。

频繁的模式应该是稳定的。但是，为了适应操作环境的变化，我们将检测器中使用的模式更新为周期性(这个更新不频繁)的离线过程(即检测器使用所发现的模式，但从不在线更新它们)。这样既可以保持在线检测的简单性，又可以避免瞬态异常现象对模式的影响。(注：我理解的是入瞬态的异常模式代表短时间内突然出现的频繁模式，所以既然不经常更新，就不会在频繁模式中加入瞬态的异常模式)

5.2 B. Estimating distributions of session durations(B.估计会话持续时间的分布)

为了实现及时的在线检测，需要知道任何给定的模式需要多长时间才能完成。为此，作者估计每个模式的会话持续时间分布。基于这个分布，我们计算每个模式的截止时间$T_{cut}$(例如，分布下99.95%满足的时间)。在此之后，该模式的大多数会话将完成。

为了选择一个适合这些的数据分布，首先观察图像3可以发现：

• 会话持续时间的直方图都是即有显著性值也是肥尾分布(fat tailed)【如图所示的两个例子(在第7节A小节表1中的模式1和2)在图3(a)和(b)】
• 幂律分布因其漂亮的数学性质[5][16]已广泛应用与长尾模型数据。这里选择它来建模数据，一个log-log图证实了数据尾部近似遵循幂律分布【图3 (c)和(d)】

为了估计分布参数，我们采用了[4]中提出的基于Kolmogorov-Smirnov (KS)统计[10]的最大似然拟合方法和拟合优度检验相结合的方法

• 在实际应用中，很少有数据集的所有值都遵循幂律分布。幂律通常只适用于大于最小值$x_{min}>0$，即分布的尾部
• 对于低于此阈值的样本，我们使用直方图作为其经验分布。因此，我们本质上使用一个包含两个分段的混合分布来建模持续时间值的分布函数：
  • 尾部的幂律分布(大于$x_{min}$的值)，权重为$w$
  • $x_{min}$以下的值使用的直方图，权重为$(1-w)$

对于只取整数值的持续时间，考虑概率分布形式是$p(x)=Pr(X=x)=Cx^{-\beta}$的情况。不难得出，归一化常数由下式计算：
$C(\beta,x_{min})=(\sum_{i=0}^{\infty}(i+x_{min})^{-\beta})^{-1}\dots(1)$
假设已知$x_{min}$($x_{min}$估计的方法的讨论在后面)，最大似然估计量(Maximum Likelihood Estimator,MLE)的尺寸参数$\beta$可以近似用下式得出：(注：后面的公式推导都可以在参考文献[4]中找到)
$\hat\beta\approx1+n[\sum_{i=1}^nln\frac{x_i}{x_{min}-0.5}]^{-1}\dots(2)$
其中$x_i,i=1\dots n$是持续时间值$x_i\ge x_{min}$时的观察值

为了估算$x_{min}$，我们选择一个值，

• 使训练数据的概率分布在$x_{min}$以上尽可能的和幂律模型最优拟合
• 使用KS统计来衡量两个分布之间的距离
• 估计值$\hat x_{min}$作为$x_{min}$的值使得两个函数之间的KS统计值最小
  • 第一个函数是训练数据在$x_{min}$取得最小值时的经验累积分布函数(Cumulative Distribution Function,CDF)
  • 第二个函数是在所有$x_i\ge x_{min}$时的训练数据最优拟合的幂律模型的CDF

【图3(c)和(d)】分别为模式1和模式2的经验分布(图中圆形的点)和拟合幂律模型(图中的实线)。由模型可知，幂律分布的CDF是$p(x)=Pr(X<x)$可以用下式得到：
$P_p(x)=1.0-C(\beta,x)/C(\beta,x_{min})\dots(3)$
其中$C(\beta,x)$在式(1)中定义，然后对于$\eta\ge1.0-w$，最大分布$\eta^{th}$百分位的值$x_\eta$满足以下公式：
$P_p(x_\eta)=(\eta-(1.0-w))/w\dots(4)$
其中$P_p(x)$在公式(3)中定义。我们在第7节中给出了模式1和模式2混合分布的估计的$99.90^{th}、99.95^{th}和99.99^{th}$百分位，以及对检测精度的改进

5.3 C. Implementation of Stage 1(C.阶段一的实现)

基于模式的检测器从日志解析器中接收事件流

• 如果一个事件是我们正在监视的一些踪迹的一部分(因为它包含一个标识符)，检测器将它与具有相同标识符的其他事件分组，并检查事件组的任何子集是否匹配(注：我感觉就是序列上的匹配)某个频繁模式
• 如果子集匹配，则从检测器的内存中删除所有匹配事件(队列中可能还剩下一些非匹配事件)。删除匹配的事件可以使内存中事件历史记录的大小保持较小，大大提高检测器的效率

在逻辑上尝试将所有事件集匹配到所有模式。这里使用最朴素的全匹配法，因为

• 这种方法在许多系统足够好用，因为模式的数量通常很小并且踪迹很短
• 此外，在使用许多长模式的情况下，可以使用更高级的数据结构，如后缀树[21]来提高匹配效率

具体的处理方法：

• 如果没有找到任何可以匹配的模式，则将事件添加到队列中，并根据事件时间戳$T$设置超时编号$T_o$(注：我的理解是这种情况表明遍历整个踪迹，都没有找到一个满足条件的会话)
• 如果事件匹配一个或多个模式，则选择截止时间最大的那个模式($T_{cut}$)，设置超时编号为$T_o = T + T_{cut}$
• 如果事件不匹配任何模式(因为事件的频率不足以包含在任何模式中)，我们将其设置超时编号为$T_o= T + T_{max}$

注意，因为$T_{cut}$通常比$T_{max}$小得多，所以该方法可以对大多数事件实现快速检测

检测规则：

• 检测器定期检查所有跟踪(当前周期设置为1秒)。该参数对检测时间影响不大，但对准确性没有影响
• 当它发现已经超时的事件时，它构造这些事件的消息计数向量(如第3节所述)并将它们发送到第二阶段基于PCA方法的检测器

这种方法背后的直觉是，只要我们能够合理地确定事件不属于任何被监视的频繁模式，它就会被传递到基于PCA的检测器，称之为非模式事件

6. STAGE 2: PCA DETECTION(阶段二：PCA检测)

从阶段1传递的非模式事件向量的噪声明显比频繁模式大。噪声来自未捕获的交错、持续时间的高度变化和真实的异常。为了从这些噪声数据中发现真正的异常，我们使用了一种基于统计异常检测方法，即PCA检测器，它在从控制台日志和许多其他系统[28]、[13]中进行离线问题检测时是比较准确的。

与频繁模式挖掘一样，主成分分析的目标是发现统计上占主导地位的模式，从而识别数据内部的异常

主成分分析可以通过自动选择一个(小的)坐标集来反映原始坐标之间的协变，从而捕获高维数据中的模式。一旦我们从归档和定期更新的数据中估计出这些模式，我们就使用它们来转换传入的数据，使异常模式更容易检测。

PCA检测也有一个模型建立阶段和一个在线检测阶段：

• 在建模阶段，PCA捕获转换矩阵$PP^T$中的主导模式，其中$P$由PCA算法选择最大特征向量对应主成分
• 在检测阶段，每条消息矢量$y$的终点到正常子空间$S_d$的“距离”来确定$y$是否异常，其中$y_a$是$y$到异常子空间$s_a$上的投影，并且可以通过$y_a=(I-PP^T )y$计算，则距离平方预测误差为$SPE=‖y_a ‖^2$
• “检测规则”很简单：如果$SPE=‖y_a ‖^2>Q_\alpha$，则标记$y$对应的消息向量是异常的

  其中$Q_α$表示在$(1-\alpha)$置信水平下SPE残差函数的阈值统计量

在实际部署中，模型可以定期更新。请注意，由于此阶段的数据比较混杂，并且非模式数据的依赖于工作负载，因此PCA的模型更新周期通常比频繁模式挖掘的模型更新周期短。

7. EVALUATION(评价)

本文使用：

• 来自Amazon EC2云计算环境中一个203节点，安装了Hadoop[1]的真实日志来评估本文的方法
• Hadoop是MapReduce框架的开源实现，用于大规模并行数据处理
• Hadoop在数据挖掘和系统研究中越来越受欢迎，因此了解其运行时行为、检测其执行异常和诊断其性能下降问题非常重要

为了将本文的在线方法与[28]中提出的离线算法直接进行比较：

• 使用了相同的日志集，其中包含超过2400万行未压缩大小为2.4GB的日志消息
• 这些日志是由运行Hadoop 48小时的203个节点生成的，完成了许多标准的MapReduce作业

  如分布式排序和文本扫描

• 机器的平均负载即有充分利用也有几乎处于空闲的状态。日志包含575,319个事件踪迹，对应于Hadoop文件中的575,319个不同的文件块

作者相信这个数据集是一个很有代表HDFS集群

在[28]中，数据集中所有的踪迹都被标记为正常或异常，并且大多数异常都有分类/解释。这为评估本文的结果提供了依据：

• 标记了超过50万个事件踪迹，因为许多踪迹是相同的(并且是正常的)，所以可以手工标记
• 实际上，数据中只有680个不同的踪迹

请注意，标记过程不考虑任何踪迹的持续时间。本节后面展示这种省略的效果

为了模拟系统操作员将如何使用本文的技术，使用以下两步方法来评估本文的方法：

• 首先，我们随机抽取10%的执行踪迹样本，在此基础上构建检测模型，包括频繁模式、模式持续时间分布和PCA检测器
• 然后我们重新跟踪整个过程，并使用导出的模型进行在线问题检测
  • 整个过程是无监督的，因为标签只是为了评估，而不是为了建立模型
  • 多次改变采样数据的子集来构建模型，得到了相同的检测结果。因为我们识别的模式很频繁，随机抽样是稳定的

需要设置两个参数:

• 最大检测延迟$T_{max}$(在第5节中定义)设置为60秒

  这意味着在可疑事件踪迹出现在日志中之后，操作者最多希望在60秒内收到可疑异常的通知

• PCA阈值参数$\alpha$(第6章描述)。设置为0.001,也就是说,我们是接受不到0.1%的所有异常的数据点

  选择的这些基线值为这些算法的公共设置(即在不了解数据的情况下的默认设置值)，但是在第7节的B小节中，展示了本文的检测结果在很大范围内对这些参数不敏感

7.1 A. Stage 1 Pattern mining results(A.阶段1模式挖掘结果)

阶段1的目标是删除与正常应用程序行为相对应的频繁模式

• 表一总结了在测试数据使用基线参数值$T_{max}=60s$下找到的频繁模式
• 识别的模式包含踪迹中所有事件的85.6%
• 因此阶段2 (PCA异常检测)最多只能考虑14.4%的事件

举例说明表的意思，该表显示模式1是分配一个写入块所对应的事件序列。踪迹中的20.3%事件被分类为属于此模式的实例，因此将被过滤掉，不会传递到阶段2。此模式的持续时间分布的99.9、99.95和99.99的百分位数分别为11秒、13秒和20秒。我们选择这些高百分位数值是因为我们希望大多数正常会话在这些间隔内完成。
注意， 即使是模式持续时间的99.99的百分位数也明显小于$T_{max}$。这一点很重要，因为检测延迟是基于模式持续时间或$T_{max}$(以较短的值为准)。由于篇幅的限制，本文仅将$T_{cut}$设置为每个模式的99.95的百分位值来显示检测结果。其他值的结果类似

具体解释相关模式：

• 模式1和2都与编写文件块相关。它们在逻辑上属于相同的操作，但是写入会话可以是任意长的：写入文件的应用程序可能在开始写入之后等待任意数量的时间，然后才真正发送数据

  由检测延迟有设定阈值，因此本文将会话的开始和结束分为两种不同的模式，以便及时检测。显然，这种分离有一定的局限性，具体将在第8节中详细讨论

• 模式4到6只包含单个事件。这些事件用于报告一些数字，并不用于基于事件跟踪的检测，因此单个事件完成操作(例如，读取等)

• 模式5由一个报告异常的事件组成，但是正如我们在[28]中讨论的那样，这确实是一个正常的操作，消息文本表示一个错误的日志记录实践，这让许多用户感到难以判断。相反，由于本文使用模式频率进行检测，因此很容易将这些异常消息识别为正常操作

7.2 B. Detection precision and recall(B.检测精度和召回率)

从[28]中获得每个事件跟踪的label/abnormal label

• 由于本文的技术是基于会话的，所以当且仅当踪迹包含至少一个异常会话时，则将其确定为异常，从而允许使用原始标签进行直接比较
• 使用精确度和召回率的标准信息检索指标来评估我们的方法
• 设TP、FP、FN分别为真阳性、假阳性、假阴性的个数。我们有:
  • 精度= TP/(TP+FP)和召回率= TP/(TP+FN)
  • 100%召回意味着没有遗漏任何实际问题
  • 100%的精确度意味着在那些确定为问题的事件中没有错误警报

在我们的数据集中，有575,319条事件踪迹，其中16,916条被标记为异常

• 表II(a)是PCA置信水平$\alpha$的变化对数据精度和召回率结果的影响【介绍】
• 表II(b)是最大检测时间延迟$T_{max}$的变化对数据精度和召回率结果的影响【介绍】
• 每个表的黑体字行表示基线值$\alpha=0.001,T_{max}= 60$【介绍】
• 结果显示在大范围的$\alpha$值和$T_{max}$值下都有100%召回率，这表明算法捕捉到了所有的手动标签的异常【优点】
• 良好的召回率主要是由于数据中的强模式：事件跟踪是程序执行逻辑(可能是确定性的和规则的)的直接表示，如日志打印语句所反映的那样。强模式允许对随机噪声有更好的容忍度，特别是在频繁模式挖掘阶段可以使用高支持来过滤掉随机交错和重排序事件【优点】
• 由于误报和一些不明确的情况，其精度并不完美【缺点】

  在第7节的D小节中与脱机结果进行比较时，将详细介绍检查的误报

• 表II(a)显示精度和召回率对$\alpha$的大范围选择时并不敏感，与论文[28]和[13]中讨论的结果一致【解释说明】
• 表II(b)显示，在某一范围内，precision和recall对最大检测延迟$T_{max}$不敏感，但是将其设置在该范围之外(表II(b)的第一行和最后一行)会对recall或precision产生负面影响【解释说明】

  直觉上，当$T_{max}$太小时，许多逻辑会话(特别是那些没有被主导模式覆盖的会话)被随机切断，而当$T_{max}$太大时，许多不相关的会话被组合成相同的消息计数向量，这给PCA检测器引入了太多的噪声。这两种影响都会降低精确度和召回率

正如第5节的B小节中所描述的，我们使用了一个相当复杂的模型来估计会话的持续时间。如果我们假设是一个简单的高斯分布，那么表I中模式1的99.95%的$T_{cut}$估计为5.3，模式2的估计为4.0，不到本文建模的分布拟合估计的结果时间$T_{cut}$的一半。使用高斯分布推导的截止时间，假警报的数量增加了45%，精度从86%下降到80%。

因此，持续时间分布估计(第5节的B小节)增加的复杂性较小，而召回率和准确率要高得多

7.3 C. Detection latency(c.检测延迟)

检测延迟(在第5节中定义)捕获检测的及时性，这是在线方法的一个关键目标。

回想一下，最小化检测延迟的困难源自这样一个事实：在发生特定事件或一组事件之前，不可能总是标记踪迹异常。 例如，表I模式1中的分配块消息仅仅表示操作序列的开始；检测器必须缓冲事件并等待进一步的事件。直到模式1的最后一个事件(例如，三个预期接收消息中的最后一个)，才会对该消息作出最终决定。然后，包含此分配块事件的跟踪的检测时间就是从发出分配块事件到检测结果生成的时间。

• 图4(左)显示了检测时间在所有事件上的累积分布函数(CDF)
• 超过80%的事件可以在几秒钟内确定为正常或异常

  这是因为我们使用截止时间$T_{cut}$来停止等待更多事件，而不是大多数事件的最大延迟$T_{max}$。一些事件需要最大允许的检测延迟：那些不匹配任何模式的事件(默认为$T+T_{max}$)。根据定义，这些事件非常罕见，因此它们较长的检测时间的总体影响是有限的

• 图4(右)显示了检测器每秒缓冲的事件数的CDF
• 由于检测时间很短，大多数事件都被快速处理并从缓冲区中删除

  因此，正如预期的那样，缓冲区中事件的数量很少

7.4 D. Comparison to offline results(D.与离线结果比较)

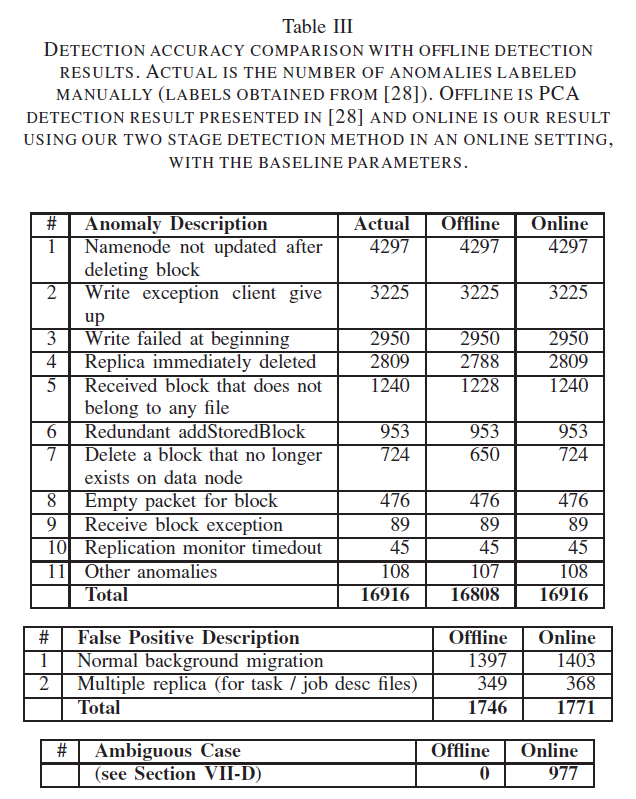
• 表3比较了文献[28]中的离线检测结果以及我们的在线检测中使用基线参数值 $\alpha= 0.001,T_{max}= 60$ 产生的结果。

• 表中第一列的错误标签是直接从[28]得到的。可以看出，我们不仅能像离线方法那样成功地捕捉到所有异常，还能得到更低的假阴性率。

  原因是，对于在线检测，我们根据时间持续时间将事件跟踪划分为多个会话，并将检测基于单个会话而不是整个踪迹。因此，发送到检测器的数据不受多个独立会话（例如，某些块的读取频率高于其他块）的应用程序相关的交错所产生的噪声的影响。

• 表III中的两种误报均为罕见但正常的事件。

  例如，假阳性#2(过度复制)是由于特殊的应用程序请求，而不是系统问题。这些确实是罕见的事件(在所有跟踪中只有368次发生)，它们对应于罕见但正常的操作。使用完全无监督的检测器很难处理这些情况。为了处理这些情况，我们允许操作人员手动添加模式来编码关于实际问题的特定于领域的知识，并过滤掉这些情况。

• 表III列举了由于异常定义不清而引起的模糊情况。

  例如，我们的在线算法将一些写入会话标记为异常，因为其中一个数据节点的响应时间远远长于其他所有节点，从而导致异常长的写入session1。从系统管理的角度来看，这些情况可能应该标记为异常，因为尽管这些块最终被正确地编写，但是这个场景有效地将整个系统的速度降低到响应最慢的节点的速度。

8. DISCUSSION(讨论)

在线检测的局限性
在线检测的一个明显的局限性是，我们无法捕获跨事件在很长时间内的相关性。

例如，正如在第7节的A小节中所讨论的，表I中的模式1和2之间存在巨大且不可预测的时间间隔，因此我们必须将它们分成两种模式。然而，这种分离的结果是我们失去了观察模式1中的事件与模式2中的匹配事件之间的相关性的能力，这可能会影响我们捕获一类新的操作问题。（例如，模式1中的事件指示有多少数据节点开始写；在模式2中，每个这样的节点都应该有一个相应的结束写入事件。）
这是在线检测固有的局限性，因为需要检测延迟。这可以通过记住更长的历史(可能以更紧凑/聚合的形式)来解决，尽管这会使检测器的设计更加复杂。
因此，我们提出了一种不同的方法：通过利用相对廉价的计算周期，我们可以对存档数据定期执行脱机检测，以发现违反此类未捕获约束的异常。

用例

• 除了显示个别异常警报之外，我们的技术还允许操作人员使用[28]中描述的解析和可视化技术，将每个警报链接回原始日志甚至相关的源代码段
• 此外，由于我们能够快速检测性能异常，操作人员有更多的时间来防止它们造成更严重的错误。确定性错误导致的异常即使在很短的时间内也会频繁地重复出现

  如表III中的异常1，它是由Hadoop源代码中的确定性错误导致的。由于每次发生的异常报警都会影响操作者的注意力，因此我们对异常进行分层聚类，并报告每种异常类型的数量。空间限制阻止了对集群方法的描述

9. CONCLUSIONS AND FUTURE WORK(结论，未来工作)

结论：

• 本文展示了如何使用两阶段数据挖掘技术来识别和过滤来自自由文本控制台日志的通用(正常)操作模式
• 对其余模式执行基于PCA的异常检测，以在操作问题出现后的几分钟内识别它们(如控制台日志中的信息所示)
• 本文方法在真实数据上进行了验证，解决了此类大型系统操作人员的一个关键需求，并且匹配或优于当前用于自由文本日志分析[28]的脱机方法

作为未来的工作：

• 计划监视来自系统多个组件(例如文件系统和使用它的应用程序)的控制台日志
• 在检测到特定问题时自动确定哪个组件产生的异常

10. REFERENCES(参考文献)

[1] D. Borthakur. The hadoop distributed file system: Architecture and design. Hadoop Project Website, 2007.

[4] A. Clauset, C. Shalizi, and M. Newman. Power-law distributions in empirical data. SIAM Review, 2009.

[9] Hellerstein J L , Ma S , Perng C S . Discovering Actionable Patterns in Event Data[J]. Ibm Systems Journal, 2002, 41(3):475-493.

[21] K. Rieck and et al. Computation of similarity measures for sequential data using generalized suffix trees. In NIPS’2007. MIT Press, Cambridge, MA, 2007.

[28] Xu W , Huang L , Fox A , et al. [ACM Press the ACM SIGOPS 22nd symposium - Big Sky, Montana, USA (2009.10.11-2009.10.14)] Proceedings of the ACM SIGOPS 22nd symposium on Operating systems principles - SOSP "09 - Detecting large-scale system problems by mining console logs[J]. 2009:117.

11. 附录

11.1 分类算法的评估方法

1. 几个常用的术语
   这里首先介绍几个常见的 模型评价术语，现在假设我们的分类目标只有两类，计为正例（positive）和负例（negative）分别是：

1)True positives(TP): 被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数（样本数）；
2) False positives(FP): 被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；
3) False negatives(FN):被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；
4) True negatives(TN): 被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。　

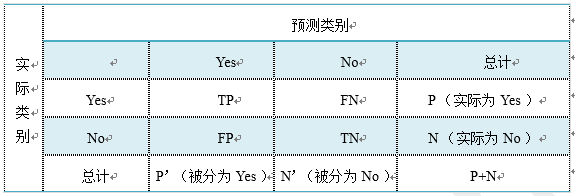
上图是这四个术语的混淆矩阵。
1）P=TP+FN表示实际为正例的样本个数。
2）True、False描述的是分类器是否判断正确。
3）Positive、Negative是分类器的分类结果，如果正例计为1、负例计为-1，即positive=1、negative=-1。用1表示True，-1表示False，那么实际的类标=TF*PN，TF为true或false，PN为positive或negative。
4）例如True positives(TP)的实际类标=1*1=1为正例，False positives(FP)的实际类标=(-1)*1=-1为负例，False negatives(FN)的实际类标=(-1)*(-1)=1为正例，True negatives(TN)的实际类标=1*(-1)=-1为负例。

2. 评价指标
   1. 正确率（accuracy）
      正确率是我们最常见的评价指标，accuracy = (TP+TN)/(P+N)，正确率是被分对的样本数在所有样本数中的占比，通常来说，正确率越高，分类器越好。
   2. 错误率（error rate)
      错误率则与正确率相反，描述被分类器错分的比例，error rate = (FP+FN)/(P+N)，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate。
   3. 灵敏度（sensitive）
      sensitive = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。
   4. 特效度（specificity)
      specificity = TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力。
   5. 精度（precision）
      精度是精确性的度量，表示被分为正例的示例中实际为正例的比例，precision=TP/(TP+FP)。
   6. 召回率（recall）
      召回率是覆盖面的度量，度量有多个正例被分为正例，recall=TP/(TP+FN)=TP/P=sensitive，可以看到召回率与灵敏度是一样的。
   7. 其他评价指标
      计算速度：分类器训练和预测需要的时间；
      鲁棒性：处理缺失值和异常值的能力；
      可扩展性：处理大数据集的能力；
      可解释性：分类器的预测标准的可理解性，像决策树产生的规则就是很容易理解的，而神经网络的一堆参数就不好理解，我们只好把它看成一个黑盒子。
   8. 查准率和查全率反映了分类器分类性能的两个方面。如果综合考虑查准率与查全率，可以得到新的评价指标F1测试值，也称为综合分类率：$F1=\frac{2 \times precision \times recall}{precision + recall}$
      为了综合多个类别的分类情况，评测系统整体性能，经常采用的还有微平均F1（micro-averaging）和宏平均F1（macro-averaging ）两种指标。宏平均F1与微平均F1是以两种不同的平均方式求的全局的F1指标。其中宏平均F1的计算方法先对每个类别单独计算F1值，再取这些F1值的算术平均值作为全局指标。而微平均F1的计算方法是先累加计算各个类别的a、b、c、d的值，再由这些值求出F1值。由两种平均F1的计算方式不难看出，宏平均F1平等对待每一个类别，所以它的值主要受到稀有类别的影响，而微平均F1平等考虑文档集中的每一个文档，所以它的值受到常见类别的影响比较大。