回到主页

目录

▶︎
all
running...

FAST GRAPH REPRESENTATION LEARNING WITH PYTORCH GEOMETRIC

本篇论文发表在ICLR 2019 (RLGM Workshop on Representation Learning on Graphs and Manifolds)，该论文也是Open Data Science总结2019第一季度的深度学习十佳论文排名第一的论文
参考资料：https://tech.sina.com.cn/csj/2019-05-07/doc-ihvhiews0329883.shtml和https://medium.com/@ODSC/best-deep-learning-research-of-2019-so-far-7bea0ed22e38

第一作者：Matthias Fey德国多特蒙德工业大学博二学生

Abstract:

1. INTRODUCTION(介绍)

首先说明图神经网络的背景意义：

1 《关系归纳偏置、深度学习和图网络》（详情请点击本行）

为什么“图网络”是近年来人工智能流行的趋势？

该论文是DeepMind联合谷歌大脑、MIT等机构27位作者发表重磅论文，提出“图网络”（Graph network），将端到端学习与归纳偏置相结合，有望解决深度学习无法进行关系推理的问题。

背景简介：

1. 人工智能、机器学习、深度学习三者的关系

1.1 为什么人工智能、机器学习、深度学习三者的关系总让人混淆？

有人说 AI 是一门最悲剧的学科，因为每当它的一个子领域发展得像模像样之后，就立马自立门户，从此和 AI “再无瓜葛”了， （Machine Learning 大概要算是最新的一个典型吧。这就让人有点奇怪，比如说数学，分门别类总算是够多了吧？可以不管怎么分，大家兄弟姐妹也都还承认自己是叫“数学”的。那 AI呢？这里有很大一部分是它自身定位的问题。）

  • AI 在一开始定了一个过高的目标，几十年后，发现情况并不像当年那么乐观，却又有些下不了台了
  • 这个时候，AI 的一些旁枝或者子领域果断放下面子， 丢掉了那个近乎玄幻的目标，逐渐发展成为“正常”的学科
  • Machine Learning 作为离家出走的典型，虽然名字里带了 Learning 一个词，让人乍一看觉得和 Intelligence 相比不过是换了个说法而已，然而事实上这里的 Learning 的意义要朴素得多。
  • 回顾Machine Learning 的典型的流程就知道了：
    • 与应用数学或者更通俗的数学建模有些类似，通常我们会有需要分析或者处理的数据，根据一些经验和一些假设，我们可以构建一个模型
    • 这个模型会有一些参数（即使是非参数化方法，也是可以类似地看待的），根据数据来求解模型参数的过程，就叫做 Parameter Estimation ，或者 Model Fitting
    • 但是搞机器学习的人，通常把它叫做 Learning （或者，换一个角度，叫 Training）——因为根据数据归纳出一个有用的模型， 这和我们人类“学习”的过程还是挺类似的吧
    • 不过，如果抛开无聊的抠字眼游戏的话，我们可以看到，Machine Learning 已经抛弃了“智能”的高帽子， 它的目的就是要解决具体的问题——而并不关心是否是通过一种“智能”的方式类解决的
    • 说到这里，其实我们构造模型就类似于写一个类，数据就是构造函数的参数，Learning 就是构造函数运行的过程，成功构造一个对象之后，我们就完成了学习

————张驰原

1.2 人工智能、机器学习、深度学习三者关系与对应发展时间

根据上一小节的介绍，下面这张关系图也就显而易见了：

如上图：

  • 人工智能是最早出现的，也是最大、最外侧的同心圆
  • 其次是机器学习，稍晚一点
  • 最内侧，是深度学习， 当今人工智能大爆炸的核心驱动。
  • 五十年代， 人工智能曾一度被极为看好
  • 之后， 人工智能的一些较小的子集发展了起来。先是机器学习，然后是深度学习
  • 深度学习又是机器学习的子集。深度学习造成了前所未有的巨大的影响。

具体来说：

  • 1956年，几个计算机科学家相聚在达特茅斯会议（Dartmouth Conferences），提出了“人工智能”的概念
  • 其后，人工智能就一直萦绕于人们的脑海之中，并在科研实验室中慢慢孵化
  • 之后的几十年，人工智能一直在两极反转， 或被称作人类文明耀眼未来的预言；或者被当成技术疯子的狂想扔到垃圾堆里。坦白说，直到2012年之前，这两种声音还在同时存在
  • 2012年Hinton课题组首次参加ImageNet图像识别大赛， 通过构建CNN的AlexNet一举夺得冠军，且碾压第二名 （SVM方法）
  • 过去几年，尤其是2015年以来，人工智能开始大爆发。很大一部分是由于GPU的广泛应用， 使得并行计算变得更快、更便宜、更有效
  • 当然，爆发也跟无限拓展的存储能力和骤然爆发的数据洪流（大数据） 的组合拳，也使得图像数据、文本数据、交易数据、映射数据全面海量爆发有关

参考资料：https://www.cnblogs.com/dadadechengzi/articles/6575767.html

2. 本论文的大背景及其意义

人工智能界有三个主要学派，符号主义（Symbolicism）、连接主义（Connectionism）、行为主义（Actionism）。

符号主义的起源，注重研究知识表达和逻辑推理。经过几十年的研究，目前这一学派的主要成果，一个是贝叶斯因果网络，另一个是知识图谱。

  • 贝叶斯因果网络的旗手是Judea Pearl 教授，2011年的图灵奖获得者。但是据说 2017年 NIPS 学术会议上，老爷子演讲时，听众寥寥。2018年，老爷子出版了一本新书，“The Book of Why”，为因果网络辩护，同时批判深度学习缺乏严谨的逻辑推理过程
  • 而知识图谱主要由搜索引擎公司，包括谷歌、微软、百度推动，目标是把搜索引擎，由关键词匹配，推进到语义匹配

连接主义的起源是仿生学，用数学模型来模仿神经元

  • Marvin Minsky 教授因为对神经元研究的推动，获得了1969年图灵奖
  • 把大量神经元拼装在一起，就形成了深度学习模型， 深度学习的旗手是 Geoffrey Hinton 教授，2018图灵奖获得者。深度学习模型最遭人诟病的缺陷，是不可解释

行为主义把控制论引入机器学习，最著名的成果是强化学习

  • 强化学习的旗手是 Richard Sutton 教授。近年来Google DeepMind 研究员，把传统强化学习，与深度学习融合， 实现了 AlphaGo，战胜当今世界所有人类围棋高手

DeepMind 发表的这篇论文，提议把传统的贝叶斯因果网络和知识图谱，与深度强化学习融合， 并梳理了与这个主题相关的研究进展。

参考资料：https://blog.csdn.net/qq_32201847/article/details/80708193

转折说明图神经网络面临的一个挑战，引出本文研究对象：

2 MIT许可相关资料图（详情请点击本行） 

                                            | pytorch     |   PyG       | tensorflow/mxnet

2. OVERVIEW(总览)

数学符号：

基本数据结构：class Data(x=None, edge_index=None, edge_attr=None, y=None, pos=None, norm=None, face=None, **kwargs)

邻接聚合。 将卷积运算符推广到不规则域通常表示为邻域聚合或消息传递模式(Gilmer et al.,2017)Neural Message Passing for Quantum Chemistry

x⃗i′=γ(x⃗i,□j∈N(i)ϕ(x⃗i,x⃗j,e⃗j,i))\vec{x}_{i}^{\prime}=\gamma\left(\vec{x}_{i}, \square_{j \in \mathcal{N}(i)} \phi\left(\vec{x}_{i}, \vec{x}_{j}, \vec{e}_{j, i}\right)\right)

其中：

在实际应用中，可以通过对节点特征的聚集和分散以及在γ\gamma和ϕ\phi函数上使用按照元素矢量化计算(vectorized element-wise computation)来实现，如图1所示。 虽然处理的是不规则结构的输入，但这种方案可以被GPU大大加速。相对于通过稀疏矩阵乘法实现，使用gather/ scatterts被证明对于低阶图和非合并输入是有利的， 并允许在聚合时集成中心节点和多维边缘信息。

作者提供了一个MessagePassing接口3^3允许使用者快速和清晰的原型供大家创造新的研究思路。
为了使用该类，用户只需要定义如下方法：

3 MessagePassing源码分析（详情请点击本行） 

import sys
import inspect

import torch
from torch_geometric.utils import scatter_

special_args = [
    'edge_index', 'edge_index_i', 'edge_index_j', 'size', 'size_i', 'size_j'
] #用于存储需要特殊对待的参数字符串的名字
__size_error_msg__ = ('All tensors which should get mapped to the same source '
                      'or target nodes must be of same size in dimension 0.') #错误提示元组
# 下面根据python版本选择用于得到运行时函数参数列表的函数（传入函数名即可）
is_python2 = sys.version_info[0] < 3
getargspec = inspect.getargspec if is_python2 else inspect.getfullargspec


class MessagePassing(torch.nn.Module):
    r"""Base class for creating message passing layers

    .. math::
        \mathbf{x}_i^{\prime} = \gamma_{\mathbf{\Theta}} \left( \mathbf{x}_i,
        \square_{j \in \mathcal{N}(i)} \, \phi_{\mathbf{\Theta}}
        \left(\mathbf{x}_i, \mathbf{x}_j,\mathbf{e}_{i,j}\right) \right),

    where :math:`\square` denotes a differentiable, permutation invariant
    function, *e.g.*, sum, mean or max, and :math:`\gamma_{\mathbf{\Theta}}`
    and :math:`\phi_{\mathbf{\Theta}}` denote differentiable functions such as
    MLPs.
    See `here <https://rusty1s.github.io/pytorch_geometric/build/html/notes/
    create_gnn.html>`__ for the accompanying tutorial.

    Args:
        aggr (string, optional): The aggregation scheme to use
            (:obj:`"add"`, :obj:`"mean"` or :obj:`"max"`).
            (default: :obj:`"add"`)
        flow (string, optional): The flow direction of message passing
            (:obj:`"source_to_target"` or :obj:`"target_to_source"`).
            (default: :obj:`"source_to_target"`)
    """

    def __init__(self, aggr='add', flow='source_to_target'):
        super(MessagePassing, self).__init__()
        # 存储聚合方案的类变量aggr
        self.aggr = aggr
        assert self.aggr in ['add', 'mean', 'max']
        # 存储图中节点映射方向的类变量flow
        self.flow = flow
        assert self.flow in ['source_to_target', 'target_to_source']
        # 得到message实际传入的参数变量名并存储在__message_args__中
        self.__message_args__ = getargspec(self.message)[0][1:]
        #筛选出变量名中的特殊参数名，即：'edge_index', 'edge_index_i', 'edge_index_j', 'size', 'size_i', 'size_j'
        #并且编号为元组的列表，eg：[(0,edge_index),(1,edge_index_j)] etc.
        self.__special_args__ = [(i, arg)
                                 for i, arg in enumerate(self.__message_args__)
                                 if arg in special_args]
        # 除去__message_args__中的特殊参数名
        self.__message_args__ = [
            arg for arg in self.__message_args__ if arg not in special_args
        ]
        # 得到update实际传入的参数变量名并存储在__update_args__中
        self.__update_args__ = getargspec(self.update)[0][2:]

    def propagate(self, edge_index, size=None, **kwargs):
        r"""The initial call to start propagating messages.

        Args:
            edge_index (Tensor): The indices of a general (sparse) assignment
                matrix with shape :obj:`[N, M]` (can be directed or
                undirected).
            size (list or tuple, optional): The size :obj:`[N, M]` of the
                assignment matrix. If set to :obj:`None`, the size is tried to
                get automatically inferrred. (default: :obj:`None`)
            **kwargs: Any additional data which is needed to construct messages
                and to update node embeddings.
        """
        # 得到图分配矩阵的大小，默认为None
        size = [None, None] if size is None else list(size)
        assert len(size) == 2
        # 根据构造时类变量flow的参数选择字典ij的内容, eg: 'target_to_source'时是{"_i": 0, "_j": 1}
        i, j = (0, 1) if self.flow == 'target_to_source' else (1, 0)
        ij = {"_i": i, "_j": j}

        message_args = []
        for arg in self.__message_args__: #遍历message实际传入的参数
            if arg[-2:] in ij.keys():  #如果参数后两个字符串是"_i"或者 "_j"
                tmp = kwargs.get(arg[:-2], None) #得到包含"_i"或"_j"的参数名的前面的字符串的变量名对应的变量值
                if tmp is None:  # pragma: no cover
                    message_args.append(tmp)
                else: #如果tmp包含内容的话，则根据self.flow得到需要处理的数据
                    idx = ij[arg[-2:]]
                    if isinstance(tmp, tuple) or isinstance(tmp, list):
                        assert len(tmp) == 2
                        if tmp[1 - idx] is not None:
                            if size[1 - idx] is None:
                                size[1 - idx] = tmp[1 - idx].size(0)
                            if size[1 - idx] != tmp[1 - idx].size(0):
                                raise ValueError(__size_error_msg__)
                        tmp = tmp[idx]

                    if size[idx] is None:
                        size[idx] = tmp.size(0)
                    if size[idx] != tmp.size(0):
                        raise ValueError(__size_error_msg__)

                    tmp = torch.index_select(tmp, 0, edge_index[idx])
                    message_args.append(tmp)
            else: #如果参数后两个字符串不是"_i"或者 "_j"
                message_args.append(kwargs.get(arg, None)) #直接从kwargs挑出对应参数的值附加到message_args中
                
        size[0] = size[1] if size[0] is None else size[0]
        size[1] = size[0] if size[1] is None else size[1]
        # 关键字参数列表kwargs中加入必选参数
        kwargs['edge_index'] = edge_index
        kwargs['size'] = size
        #message_args 中加入特殊参数
        for (idx, arg) in self.__special_args__:
            if arg[-2:] in ij.keys():
                message_args.insert(idx, kwargs[arg[:-2]][ij[arg[-2:]]])
            else:
                message_args.insert(idx, kwargs[arg])
        #update_args 中保存update函数的传入参数
        update_args = [kwargs[arg] for arg in self.__update_args__]
        # 这一块对应论文中的图片！
        out = self.message(*message_args)
        #下面这个函数使用https://github.com/rusty1s/pytorch_scatter包中的方法，该方法解释如下：
        #一个小型扩展库，其中包含用于PyTorch的高度优化的稀疏更新(scatter)操作，
        #这些操作在主包(Pytorch)中没有。散点运算可以粗略地描述为基于给定的“群指数”张量的约简运算。



        out = scatter_(self.aggr, out, edge_index[i], dim_size=size[i]) #该论文的优化点
        out = self.update(out, *update_args)
        
        return out

    def message(self, x_j):  # pragma: no cover
        r"""Constructs messages in analogy to :math:`\phi_{\mathbf{\Theta}}`
        for each edge in :math:`(i,j) \in \mathcal{E}`.
        Can take any argument which was initially passed to :meth:`propagate`.
        In addition, features can be lifted to the source node :math:`i` and
        target node :math:`j` by appending :obj:`_i` or :obj:`_j` to the
        variable name, *.e.g.* :obj:`x_i` and :obj:`x_j`."""

        return x_j

    def update(self, aggr_out):  # pragma: no cover
        r"""Updates node embeddings in analogy to
        :math:`\gamma_{\mathbf{\Theta}}` for each node
        :math:`i \in \mathcal{V}`.
        Takes in the output of aggregation as first argument and any argument
        which was initially passed to :meth:`propagate`."""

        return aggr_out

A. 几乎所有最近提出的邻域聚合函数都可以使用这个接口，包括（但不限于）已经集成到PyG中的方法：

B. 用于学习点云、流形和具有多维边缘特征图形的方法：

C. 除了以上这些操作符，PyG还提供高等级级的函数实现：

全局池化 PyG还支持图形级输出，而不是节点级输出，它支持各种读取函数，如全局添加、平均值或最大池。还提供更复杂的方法：

层次池化 为了进一步提取层次信息并允许更深层次的GNN模式，可以以空间或数据依赖的方式应用各种池方法。目前提供了以下实现：

小批量处理 PyG的框架通过自动创建单个（稀疏）块对角邻接矩阵和连接节点维中的特征矩阵，支持批量的多个图实例（大小可能不同）。因此，无需修改即可应用邻域聚合方法，因为断开连接的图之间不交换任何消息。此外，自动生成的赋值向量确保节点级别的信息不会跨图聚合，例如，当执行全局聚合操作符时。

数据集处理 PyG提供了一个一致的数据格式和易于使用的接口来创建和处理数据集，既适用于大型数据集，也适用于训练期间可以保存在内存中的数据集。为了创建新的数据集，用户只需要读取/下载他们的数据，并在各自的process方法中将其转换为PyG数据格式。此外，数据集可以通过使用transforms方法来修改，转换采用单独的图形并对其进行转换，例如，用于数据增强，用于使用合成结构图属性增强节点特征(Cai &Wang, 2018)A simple yet effective baseline for non-attributed graph classification(LocalDegreeProfile函数)，从点云自动生成图或从网格中采样点云。
xi=xi∥(deg⁡(i),min⁡(DN(i)),max⁡(DN(i)),mean⁡(DN(i)),std⁡(DN(i)))\mathbf{x}_{i}=\mathbf{x}_{i} \|(\operatorname{deg}(i), \min (D N(i)), \max (D N(i)), \operatorname{mean}(D N(i)), \operatorname{std}(D N(i)))
对于节点特征，其中DN(i)={deg⁡(j)∣j∈N(i)}D N(i)=\{\operatorname{deg}(j) | j \in \mathcal{N}(i)\}。

PyG已经支持许多常见的基准数据集，这些数据集通常在文献中找到，它们在第一次实例化时自动下载并处理。其中提供了60多个图的核基准数据集https://ls11-www.cs.tu-dortmund.de/staff/morris/graphkerneldatasets：

3. EMPIRICAL EVALUATION(实证性评估)

通过对相同评价场景的综合比较研究，评价了所实现方法的正确性。所有使用过的数据集的描述和统计可以在附录b中找到。对于所有的实验，都尽可能地遵循相关论文的超参数设置。可以派生出单独的实验设置，并且可以从GitHub储存库中提供的代码复制出相应的组件。

半监督节点分类问题

本小节展示了半监督节点分类问题，见表一。实验分两块：

几乎所有的实验都显示了各自论文报告结果的高可重复性。 然而，当使用随机数据分割时，所有模型的测试性能都更差。在实验中，APPNP操作(Klicpera et al.， 2019)的性能一般最好，ARMA，SGC，GCN，GAT方法其次。

图分类问题

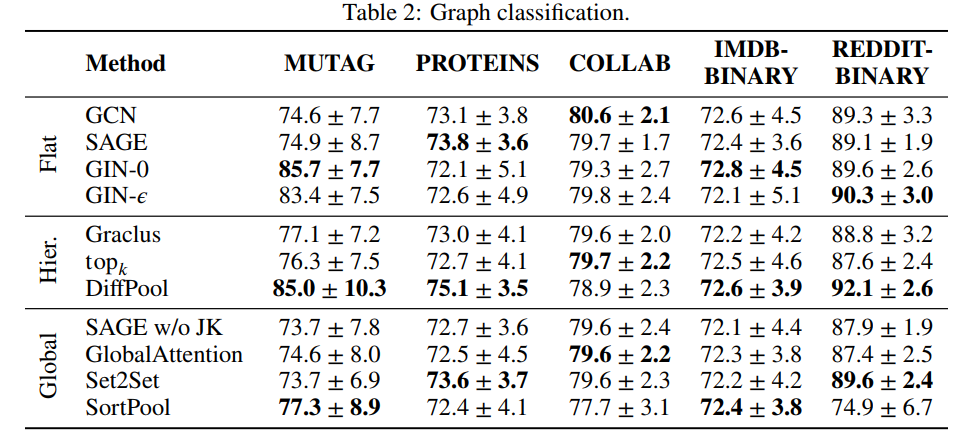
本小节展示了一些常见基准数据集进行10折交叉验证得到的平均精度（表2），具体设置如下：

由于评估和网络架构进行了统一标准化，因此并不是所有的结果都与其对应论文中展示的值一致。例如：

点云分类问题

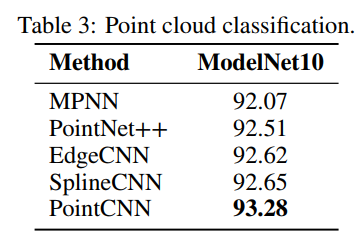
本小节评估不同的点云的方法ModelNet10(Wu et al ., 2015)并从网格表面均匀样本1024点基于面临区域（表3）：

运行时实验

对多个数据模型对进行了多次实验：

4. ROADMAP AND CONCLUSION(技术路线及结论)

5. 附录

5.1 流形

注：此部分参考张驰原的博客(ICLR 2017 BestPaper/Mxnet(16K Star)主要开发者)

Manifold Learning 或者仅仅 Manifold 本身通常就听起来颇有些深奥的感觉，有时候经常会在 paper 里看到 嵌入在高维空间中的低维流形。不过如果并不是想要进行严格的理论推导的话，也可以从许多直观的例子得到一些感性的认识。

5.1.1 示例一

因为高维的数据对于我们这些可怜的低维生物来说总是很难以想像，所以最直观的例子通常都会是嵌入在三维空间中的二维或者一维流形。

比如说一块布，可以把它看成一个二维平面，这是一个二维的欧氏空间，现在我们（在三维）中把它扭一扭，它就变成了一个流形（当然，不扭的时候，它也是一个流形，欧氏空间是流形的一种特殊情况）。

所以，直观上来讲，一个流形好比是一个 dd 维的空间，在一个 mm 维的空间中 (m>d)(m > d) 被扭曲之后的结果。 需要注意的是，流形并不是一个“形状”，而是一个“空间”，如果你觉得“扭曲的空间”难以想象，那么请再回忆之前一块布的例子。

广义相对论似乎就是把我们的时空当作一个四维流（空间三维加上时间一维）形来研究的，引力就是这个流形扭曲的结果。

当然，这些都是直观上的概念，其实流形并不需要依靠嵌入在一个“外围空间”而存在，稍微正式一点来说，一个 dd 维的流形就是一个在任意点处局部同胚于（简单地说，就是正逆映射都是光滑的一一映射）欧氏空间 RdR^d 。

实际上，正是这种局部与欧氏空间的同胚给我们带来了很多好处，这使得我们在日常生活中许许多多的几何问题都可以使用简单的欧氏几何来解决，因为和地球的尺度比起来，我们的日常生活就算是一个很小的局部。

5.1.2 示例二

那么，除了地球这种简单的例子，实际应用中的数据，怎么知道它是不是一个流形呢？于是不妨又回归直观的感觉。再从球面说起，如果我们事先不知道球面的存在，那么球面上的点，其实就是三维欧氏空间上的点，可以用一个三元组来表示其坐标。但是和空间中的普通点不一样的是，它们允许出现的位置受到了一定的限制， 具体到球面，可以可以看一下它的参数方程：

x=x0+rsin⁡θcos⁡φy=y0+rsin⁡θsin⁡φ(0≤φ≤2π and 0≤θ≤π)z=z0+rcos⁡θ\begin{aligned} x &=x_{0}+r \sin \theta \cos \varphi \\ y &=y_{0}+r \sin \theta \sin \varphi &(0 \leq \varphi \leq 2 \pi \text { and } 0 \leq \theta \leq \pi) \\ z &=z_{0}+r \cos \theta \end{aligned}

可以看到，这些三维的坐标实际上是由两个变量 θ\theta 和 φ\varphi 生成的，也可以说成是它的自由度是二，也正好对应了它是一个二维的流形。

5.1.3 示例三

有了这样的感觉之后，再来看流形学习里经常用到的人脸的例子，就很自然了。下图是Isomap 论文A Global Geometric Framework for Nonlinear Dimensionality Reduction(2000 science,1.2w被引)里的一个结果：

目前，把流形引入到机器学习领域来主要有两种用途：

这里 Isomap 正巧是一个非常典型的例子，因为它实际上是通过“改造一种原本适用于欧氏空间的算法”，达到了 “将流形映射到一个欧氏空间” 的目的。 Isomap 所改造的这个方法叫做 Multidimensional Scaling (MDS) ，MDS 是一种降维方法，它的目的就是使得降维之后的点两两之间的距离尽量不变（也就是和在原是空间中对应的两个点之间的距离要差不多）。只是 MDS 是针对欧氏空间设计的，对于距离的计算也是使用欧氏距离来完成的。如果数据分布在一个流形上的话，欧氏距离就不适用了。

5.1.4 更多的思考

Isomap主要做了一件事情，就是把 MDS 中原始空间中距离的计算从欧氏距离换为了流形上的测地距离。当然，如果流形的结构事先不知道的话，这个距离是没法算的，于是 Isomap 通过将数据点连接起来构成一个邻接图 来离散地近似原来的流形，而测地距离也相应地通过图上的最短路径来近似了。如下图所示：

这个东西叫做Swiss Roll（瑞士卷），姑且把它看作一块卷起来的布好了：

除了 Isomap 之外，Manifold Embedding 的算法还有很多很多，包括：

哪个好哪个坏也不好说，它们都各有特点，而且也各自有不少变种。

另一方面是改造现有算法使其适合流形结构甚至专门针对流形的特点来设计新的算法，比较典型的是 graph regularized semi-supervised learning 。简单地说，在 supervised learning 中，我们只能利用有 label 的数据，而（通常都会有很多的）没有 label 的数据则白白浪费掉。

在流形假设下，虽然这些数据没有 label ，但是仍然是可以有助于 Learn 出流形的结构的，而学出了流形结构之后实际上我们就是对原来的问题又多了一些认识，于是理所当然地期望能得到更好的结果！

当然，所有的这些都是基于同一个假设，那就是数据是分布在一个流形上的（部分算法可能会有稍微宽松一些的假设）

然而 real world 的数据，究竟哪些是分别在流形上的呢？这个却是很难说。不过，除了典型的 face 和 hand written digit 之外，大家也有把基于流形的算法直接用在诸如 text 看起来好像也流形没有什么关系的数据上，效果似乎也还不错。

话说回来，虽然和实际应用结合起来是非常重要的一个问题，但是也并不是决定性的，特别是对于搞理论方面的人来说。对于他们来说，其实也像是在做应用，不过是把数学里的东西应用到机器学习所研究的问题里来，而且其中关系错综复杂，图论、代数、拓扑、几何……仿佛是十八路诸侯齐聚一堂，所以让人总觉得要再花 500 年来恶补数学才行！

≡