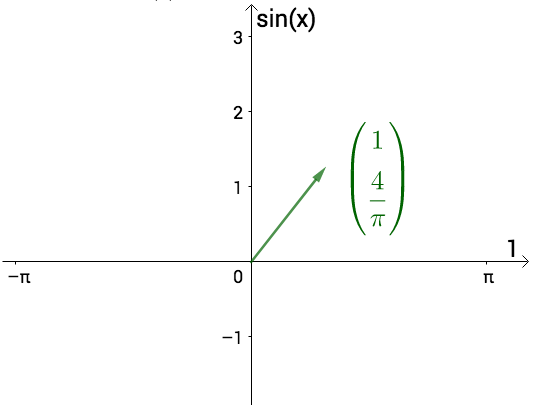回到主页

目录

• 目录
  • 科学家的小故事
    • 起源篇
    • 法国篇
    • 结尾篇
  • 理解传递公式的预备知识
    • 1 拉普拉斯矩阵
    • 2 傅里叶变换与其对Graph上的傅里叶变换的推广
      • 2.1 图上的傅里叶变换
      • 2.2 图上的傅里叶逆变换
    • 3 卷积
    • 4 卷积定理
    • 5 推广到图上
    • 6 深度学习中的图卷积
      • 6.1 第一代图卷积
      • 6.2 第二代图卷积
      • 6.3 利用Chebyshev多项式递归计算卷积核
  • 附录 傅里叶变换
  • 1 什么是空间
    • 1.1 度量空间(Metric space)
    • 1.2 向量空间(Vector space)
      • 1.2.1 线性代数的代数结构
      • 阿贝尔群（可交换群）
        • 实例1：
        • 实例2：
        • 结论
      • 不可交换群
      • 体（域）
      • 向量空间的定义
      • 1.3 赋范向量空间(Normed vector space)
      • 1.4 内积空间(Inner product space)
      • 1.5 总结
    • 2 函数空间
    • 3 从傅立叶级数到傅立叶变换
      • 3.1 傅立叶级数
        • 3.1.1 傅立叶级数是向量
        • 3.1.2 频域图
      • 3.2 非周期函数
      • 3.3 傅立叶变换

科学家的小故事

以下内容参考：数学传奇1——群星闪耀时

---

起源篇

【图论的开创】

• 1736年， 时年29岁的莱昂哈德·欧拉（Leonhard Euler）向圣彼得堡科学院递交了题为《哥尼斯堡之七桥》的著名论文，长期悬而未决的哥尼斯堡七桥问题被彻底破解，该篇论文也被认为是标志图论创立的代表性文献。

【拉格朗日的降生】

• 同年，在遥远的亚平宁半岛上，约瑟夫-路易斯·拉格朗日（Joseph-Louis Lagrange）呱呱坠地。
  • 拉格朗日的曾祖父是一名法国军官， 后移居至意大利都灵，与当地人结婚后诞下了拉格朗日的祖父
  • 拉格朗日的父亲曾经负责掌管国王军队的金库，并在都灵的公共工程建设机构担任税务官。
  • 拉格朗日本应过上优裕、富足的童年生活，无奈他的父亲却在经商过程中，不幸破产，致使家道中落
  • 像其他望子成龙的父亲一样，拉格朗日的父亲一心想把自己的儿子培养成为一名律师， 但拉格朗日本人却对法律毫无兴趣。 事实上，在都灵大学就读时，拉格朗日最初对数学也不感兴趣。 直到17岁时，他读到了英国天文学家、数学家哈雷的介绍牛顿微积分的文章后，才逐渐迷上了数学。（证明数学从微积分开始才展现出无穷魅力）
• 拉格朗日早年的数学研究到底师承何方，至今成谜。或许也只有这样，才能符合一名旷世奇才理应无师自通这样的假设

【变分法的开创】

• 现在唯一确定的是，1755年，拉格朗日曾经给已经功成名就的欧拉写信讨论数学问题，彼时拉格朗日只有19岁。 在给欧拉的信中，拉格朗日发展了欧拉所开创的变分法，用纯分析的方法求变分极值。 欧拉在回信中对拉格朗日的成果大加称赞。这使拉格朗日在都灵声名大振，并让他在19岁时就当上了都灵皇家炮兵学校的教授。 欧拉和拉格朗日两人共同奠定了变分法的理论基础，相关成果后来被称为欧拉-拉格朗日方程， 这也标志着变分法的创立。

【拉格朗日德国任职】

• 八年后的1763年， 拉格朗日在巴黎游历期间，拉格朗日首次见到了达朗贝尔，这位前辈对拉格朗日也是青睐有加
• 两年后的1765年， 达朗贝尔在给普鲁士国王腓特烈大帝的信中热情赞扬拉格朗日，并建议在柏林给拉格朗日安排一个荣誉职位。 腓特烈大帝欣然应允，他认为在 “欧洲最伟大之王”的宫廷中理应有“欧洲最伟大的数学家”。
• 但拉格朗日出于对欧拉的尊敬，不愿与其争辉而婉拒。 闻听此事的欧拉毫不犹豫地展现了其豁达平易和高风亮节的一面，于次年主动离开柏林，远赴圣彼得堡。（欧拉1707年4月15日出生于瑞士的巴塞尔，1783年9月18日于俄国圣彼得堡去世。）
• 1766年3月， 达朗贝尔给欧拉写信说明情况，拉格朗日为欧拉的有意成全深深感动遂同意了前往柏林的邀约。
• 同年5月3日欧拉离开柏林后，拉格朗日正式接受普鲁士邀请，并于8月21日离开都灵来的柏林。在柏林期间，拉格朗日深受腓特烈大帝赏识。
• 腓特烈大帝还多次向拉格朗日传授健康规律之生活的益处。 拉格朗日深深地认可国王的建议，并在自己日后的研究和生活中努力践行这一金玉良言。健康规律的生活也间接提升了拉格朗日的工作效率， 在柏林期间，他完成了大量重要的研究成果，为一生研究中的鼎盛时期，其中多数论文都发表在柏林科学院和巴黎科学院的刊物中。（健康的身体有助于科研）

【拉格朗日法国任职】

• 1786年， 与拉格朗日交好的腓特烈大帝去世，一向重情重义的拉格朗日难免触景伤情， 越发想离开柏林这块伤心地。于是，在第二年，他决定接受巴黎科学院的邀请， 动身前往法国开始工作，并于7月底到达巴黎。

---

法国篇

【一篇论文引发的血案】

• 1789年，法国大革命爆发，1793年， 革命政府决定以生于敌国为由逮捕拉格朗日，在化学家拉瓦锡的竭力保护之下，他才逃过一劫。
• 但厄运很快就降临到了拉瓦锡自己身上，而这个祸根早在十年之前就已经埋下。彼时，青年科学家马拉向法兰西科学院提交了一篇关于新燃烧理论的论文，希望可以加入科学院，但作为燃烧理论权威的拉瓦锡对这篇论文评价却很低， 导致马拉未能得偿所愿。法国大革命爆发后，雅克宾派掌权，已经成为雅克宾派领导人的马拉似乎对当年的事情仍然耿耿于怀。他在一本抨击旧制度下税务官的小册子中，专门指责曾经担任过税务官的拉瓦锡为了盘剥百姓，而向烟草上洒水增加重量。 但事实是拉瓦锡是为了防止烟草干燥才要求洒水，并且在洒水之前要称重，所有交易以干重为标准。 但在有意的煽动下，使得民众对税务官的仇恨旋即达到了顶峰
• 1794年拉瓦锡被捕，5月8日被定罪， 而且就在当天便同其他27名税务官一起被送上了断头台。在得知他的死讯之后，拉格朗日惋惜道：“他们只一瞬间就砍下了这颗头，但再过一百年也找不到像他那样杰出的脑袋了。 ”法国大革命结束后，拉瓦锡很快就被平冤昭雪，重新认定为无罪，但一切都为时已晚，这位被后世尊称为“近代化学之父”的伟大科学家已经永远地停止了思考。

【法国最著名两所学校的成立】

• 就在拉瓦锡去世的同一年， 巴黎成立了两个共和国最高学府：巴黎高等师范学院和巴黎综合理工大学
• 第二年， 拉格朗日开始于此两所高校任教，成为首批教授。小他十三岁的拉普拉斯也曾在这两所学校任教
• 二人先后培养出了多位杰出的数学家，其中就包括著名的傅立叶、泊松和柯西。

【拿破仑与数学家】

• 1799年11月， 政治强人拿破仑通过雾月政变登上历史舞台，结束了大革命以来各种恐怖局面轮番交替的形势。五年之后的1804年，拿破仑称帝，并建立法兰西第一帝国
• 军人出身的拿破仑，在主政时期，非常注重科学研究，尊重科学家。他认为：“一个国家只有数学蓬勃的发展，才能展现它国力的强大。数学的发展和至善与国家繁荣昌盛密切相关。”
• 彼时拿破仑与法国的多位数学大师都过从密切、相交甚笃。例如，他曾拜拉普拉斯为师，向其求教，还任命他为自己的内政部长。在更早的1798年，拿破仑远征埃及时，跟随其左右的傅立叶就曾因在军中表现突出而受到这位政治新星的赏识，在拿破仑掌权之后，他便任命傅立叶为格伦诺布尔省省长。

【痴迷热学的傅立叶】

• 1822年，傅立叶完成了他最重要的传世著作——《热传导的解析理论》。这本经典文献记述了他在研究热的传播时所创立的一套数学理论，也就是今日被称为“傅立叶分析”的重要数学方法
• 由于傅立叶极度痴迷热学，他认为热能包治百病， 于是在一个夏天，他关上了家中的门窗，穿上厚厚的衣服，坐在火炉边，于是他被活活热死了，1830年5月16日卒于法国巴黎

【左右逢源的拉普拉斯】

• 尽管这一时期法国历史风云巨变，但拉格朗日在政治上的表现却相当低调和沉郁。与此形成鲜明对比的是，他的同事、数学家和天文学家皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace，1749~1827）却完全是另外一种风格。拉普拉斯不仅是数学上的大师，而且在政治上也左右逢源，无论谁上台，他都能始终屹立不倒。 拉普拉斯不仅担任过拿破仑的老师，并在其主政时期，当过六个星期的内政部长
• 拉普拉斯即使在席卷法国的政治变动中，包括拿破仑的兴起和衰落，也都没有使其受到显著影响，他甚至还在拿破仑皇帝时期和路易十八时期两度获颁爵位。 但不可否认他崇高的学术威望以及他将数学应用于军事问题的才能 在动荡的政治中保护了他
• 拉普拉斯在天文学和数学上的造诣极深，素有法国的牛顿之称。现在信号处理中普遍使用的拉普拉斯算子以及拉普拉斯变换都源于他的研究

【落落寡合的柯西】

• 奥古斯丁·路易·柯西（Augustin Louis Cauchy，1789~1857）法国著名数学家。数学中的很多定理和公式都以他的名字来称呼，例如我们熟知的柯西不等式、柯西中值定理，以及柯西收敛定理等等
• 柯西的父亲曾与当时法国的大数学家拉格朗日 与拉普拉斯交往密切。柯西少年时代的数学才华颇受这两位数学家的赞赏，并预言柯西日后必成大器
• 拉格朗日还建议他的父亲在他学好文科前不要学数学，其父因此加强了对柯西的文学教养，使他在诗歌方面也表现出很高的才华
• 柯西在纯数学和应用数学上的功力相当深厚，而在数学写作上，他是被认为在数量上仅次于欧拉的人，柯西一生大约写了八百篇论文，柯西全集有27卷之多
• 但作为久负盛名的科学泰斗，柯西落落寡合，也因此常常忽视青年学者的创造。其中最令人扼腕的是，十九世纪两大青年数学天才阿贝尔与伽罗瓦的开创性的论文手稿均因柯西而“失落”，造成群论晚问世约半个世纪

---

以下内容参考：被柯西坑了的两个天才数学家——阿贝尔和伽罗瓦

• 尼尔斯·亨利克·阿贝尔（Niels Henrik Abel）和埃瓦里斯特·伽罗瓦（Évariste Galois）并称为现代群论的创始人，而两个本来前途无量的年轻人，却都英年早逝，也常使后人唏嘘不已

【穷困潦倒的阿贝尔】

• 阿贝尔（Niels Henrik Abel，1802年8月5日─1829年 4月 6日）是十九世纪挪威出现的最伟大数学家。他的父亲是挪威一个小村庄的牧师，全家生活在穷困之中。 1820年，阿贝尔的父亲去世，照顾全家七口的重担突然交到还在读大学的阿贝尔的肩上
• 所幸他在读的奥斯陆大学的老师们都没放弃这位天才，他们一起资助了阿贝尔。阿贝尔勤奋自学，一边还花大量时间作研究，研究方向就包括了四次以上方程的求解。当时意大利的数学家鲁菲尼以五百多页的证明对一元五次方程求解做了论述， 并在柯西的推动下发展出了最初的置换群思想
• 年仅22岁的阿贝尔在置换群思想帮助下，发表了《一元五次方程没有代数一般解》的论文， 论文不仅以数万字的内容代替了鲁菲尼五百多页的证明，甚至还做了许多的补充。可是他实在付不起印刷的钱（说明发论文需要一定的财力基础）， 于是数万字的论文稿再次被压缩成6页纸。阿贝尔将这6页论文寄往各地著名的数学家，希望能够得到肯定
• 阿贝尔苦苦等待，却得不到回复。所幸一年前发表的第一篇论文为他争取到了一笔政府的进修资助金。阿贝尔带上这笔钱，开始造访各地名家：
  • 他在德国柏林拜访数学王子高斯时，高斯根本不相信阿贝尔能够用6页解答这个超级数学难题
  • 阿贝尔随后来到巴黎，科学院秘书读了阿贝尔完整论文的引言，心里已经是感觉到了震惊异常，随即委托柯西审查。 可哪知道他一不留神就把阿贝尔推进了柯西的深坑里
  • 前文提到的柯西在数学上特别高产，可谁都知道柯西除了高产还有一个特点：他写的论文都特别长。 为此数学杂志都不够位置刊登他的论文，他一怒之下办了专刊，专门发表自己的论文 （一般人写论文按篇算的，牛人写论文按本算的）。
  • 当柯西拿到一份6页的论文时，他根本提不起重视的心情。他欢脱的带着稿件回了家，可事后竟然记不起放在什么地方！（说明有时候论文并不一定写得越多越好，不要忽视短小的论文）
• 阿贝尔在巴黎受尽了冷落：住着不便宜的公寓，论文的事迟迟没有回应，他处境越发难堪。最终政府的资助金用完了，阿贝尔无奈只得和亲戚借了一小笔钱，准备回挪威。而他不知道的是，此时他在巴黎不小心染上的感冒其实是肺结核
• 辗转回到挪威的阿贝尔，欠下不少钱债。他只好靠教书及收取大学的微薄津贴为生。一边维持生计还要一边偿还之前欠下的钱债
• 但他的穷困及病况并没有减低他对数学的热诚，他在这段期间写了大量的论文，主要是方程理论及椭圆函数，也就是有关阿贝尔方程和阿贝尔群的理论。他比雅可比（Jacobi）更快完全了椭圆函数的理论
• 还债和维持生计已经费尽全力，至于那总好不了的“感冒”已经无力治疗，阿贝尔的病逐渐严重起来。直至1829年4月6日凌晨，年仅27岁阿贝尔去世了， 他的未婚妻坚持不要他人之助照顾阿贝尔，“单独占有这最後的时刻”。直到阿贝尔去世前不久，人们才认识到他的价值
• 1828年，四名法国科学院院士上书给挪威国王，请他为阿贝尔提供合适的科学研究位置，在阿贝尔死後两天，阿贝尔的家人收到柏林大学数学教授的聘书， 可惜已经太迟，一代天才数学家已经在收到这消息前去世了。此后荣誉和褒奖接踵而来，1830年他和卡尔·雅可比共同获得法国科学院大奖
• 阿贝尔短暂的一生留下的著作是不多的，但他所作出的贡献却是巨大的，意义也是深远的，正如数学家埃尔米特所说：“阿贝尔所留下的思想，可供数学家们工作150年。”

【时运不济的伽罗瓦】

• 这时，另一位少年天才伽罗瓦在法国刚满18岁。他并不知道在远方的挪威，年轻的阿贝尔去世了。如果他知道 阿贝尔和他一样得出了四次以上的方程式的求解方法，他一定会感到天才之征途不孤独吧。 伽罗瓦比阿贝尔小9岁，他出生在一个善良、智慧的家庭
• 他的父亲在他4岁那年便竞选当上了市长，这让他的生活过的还算充裕。他在18岁这年， 通过自己的努力在代数方程领域取得巨大成果，正是伟大的群论。 似乎冥冥天意让伽罗瓦替阿贝尔完成未完的工作，群论完美的弥补了阿贝尔理论上的不足。这足以震撼世界的学术成果， 在呈交法国科学院之后，极巧的又碰上了柯西负责审阅
• 柯西则计划对伽罗瓦的研究成果在科学院举行一次全面的意见听取会。当他将伽罗瓦的研究成果带回家后，竟不小心连同摘要都弄丢， 原计划的听取会只得宣读了一篇他自己的论文。至于伽罗瓦的研究成果？已经因为意外“事故”无法宣读了。 看来伽罗瓦不只是接替了阿贝尔的代数工作，甚至还接替了阿贝尔的倒霉
• 伽罗瓦的家庭在这时遭遇了巨变，他的父亲在新一轮的选举中被对手暗中设局陷害，他父亲不堪其辱，选择了自杀。 这让知晓一切的伽罗瓦感到极度痛苦，父亲的冤死，让他选择了和共和主义站在一起，极端的政治观把伽罗瓦变得极爱作死。
• 1830年爆发了七月革命， 伽罗瓦所在的高等师范学院的校长将学生以禁止参与革命锁在高墙内。伽罗瓦此时政治的心那是熊熊燃烧，对校长的不满变成了校报上一篇言辞激烈的抨击文。校长也毫不客气的将伽罗瓦逐出校门。 之后激进伽罗瓦，两次被陷害入狱
• 备受不公的伽罗瓦在狱中他爱上了一个医生的女儿，伽罗瓦没想到的是，她居然有未婚夫，而她的未婚夫是一位和他一起入狱的军官。同伽罗瓦一样，这位军官也是一位激进的共和党人，伽罗瓦和对方争执，还主动提出要以决斗定胜负
• 等到伽罗瓦情绪平复的时候，才发现自己毫无胜算。怎么会和一个玩枪的行家决斗？ 伽罗瓦来不及害怕：连夜写信给他的朋友们，将自己所有在数学上的结果写了下来，期间不停在纸的空白处写上“我没有时间”。 第二天，伽罗瓦如约赴战。子弹穿过了他的腹部，他最终死在了情敌手下，年仅21岁。至此，两个数学界的天才在三年里相继离世
• 伽罗瓦的一生才华横溢，无奈天妒英才。但令后人感佩的是，在各种磨难和波折下，在如此短暂而有限的生命里，他仍然不忘数学研究，用群论彻底解决了根式求解代数方程的问题，而且由此发展了一整套关于群和域的理论，后人们称之为伽罗瓦群和伽罗瓦理论

---

结尾篇

【群论的问世】

• 直到十数年后，其他的数学家找到了阿贝尔遗失在柯西家的手稿，也研究了伽罗瓦的信件。两位早逝的天才留下的财富让世人震惊群论推迟了半个世纪问世，最终在数学家刘维尔的推动下才让数学界承认这两位天才的杰作
• 此时的柯西已经年过四十，不再进行数学研究工作，只作为一个普通的教授教书育人。当他回忆当年，曾有两个不世的天才与他擦身而过。他余下人生教书育人也无法弥补这个巨大的遗憾了
• 柯西临死前曾说过，“人总是要死的，但是，他们的功绩永存”。说的是啊，阿贝尔和伽罗瓦都死了，他们的功绩差一点就永存在柯西家的角落里了

【总结】

• 法国数学大爆发的十八至十九世纪， 很难想象在那个短暂的时间和有限的空间中，居然汇集了如此之多的数学大师。 这其中的每个人放到任何国家无疑都是引领整个时代的学术巨擘
• 但历史的巧合让他们如此戏剧化的聚合到了一起，恰似那群星闪耀的时刻， 并由此也奠定了法国在数学领域的强大地位
• 自拉格朗日以来，法国数学的影响随着一代代门徒薪火相传而深远地扩散，至今不绝。
  • 泊松的学生米歇尔·沙勒是让·加斯东·达布（Jean Gaston Darboux）的老师
  • 达布的两个学生古萨（Édouard Goursat）和埃米尔·皮卡（Émile Picard）又是雅克·阿达马（Jacques Hadamard）的老师。信号处理中的沃尔什-阿达马变换 即源自阿达马的研究
  • 阿达马的学生保罗·列维（Paul Lévy）在证明概率论里的中央极限定理过程中给出了著名的林德贝格-列维中央极限定理
  • 列维的学生迈克尔·鲁文（Michel Loève）提出了著名的KL变换， 它的另外一个名字就是我们在降维中讨论的主成分分析（PCA）
  • 鲁文的学生里奥·布瑞曼（Leo Breiman）则是著名的CART(Classification And Regression Tree)算法以及随机森林 的发明人。此外，他之于机器学习（特别是其中的集成学习领域）的重要贡献还包括Bagging以及关于Boosting的理论 探索

理解传递公式的预备知识

以下内容参考：如何理解 Graph Convolutional Network（GCN）？

1 拉普拉斯矩阵

对于图$G=(V, E)$，其Laplacian矩阵定义为$L=D-A$，其中$L$是Laplacian矩阵，$D$是顶点的度矩阵（对角矩阵），对角线上元素依次为各个顶点的度，$A$是图的邻接矩阵。

常用的拉普拉斯矩阵有三种：

$L=D-A$定义的Laplacian 矩阵更专业的名称叫Combinatorial Laplacian

$L^{s y s}=D^{-1 / 2} L D^{-1 / 2}=I-D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$定义的叫Symmetric normalized Laplacian，很多GCN的论文中应用的是这种拉普拉斯矩阵

$L^{r w}=D^{-1} L$定义的叫Random walk normalized Laplacian,

GCN的核心基于拉普拉斯矩阵的谱分解注：矩阵的谱分解，特征分解，对角化都是同一个概念，文献中对于这部分内容没有讲解太多。不是所有的矩阵都可以特征分解，其充要条件为n阶方阵存在n个线性无关的特征向量； 拉普拉斯矩阵是半正定对称矩阵（对称矩阵一定有n个线性无关的特征向量，半正定矩阵的特征值一定非负，对阵矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵。详细证明地址）。

因此，拉普拉斯矩阵一定可以谱分解，且分解后有特殊的形式。

拉普拉斯矩阵其谱分解为：

$L=U\begin{bmatrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{bmatrix}U^{-1}$

其中$U=\left(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}, \cdots, \overrightarrow{u_{n}}\right)$，是列向量为单位特征向量的矩阵，即$\overrightarrow{u_{l}}$是列向量。
$\begin{bmatrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{bmatrix}$是n个特征值构成的对角阵。

$U$是正交矩阵，因此有$UU^T=E$。

特征值分解可以写作：

$L=U\begin{bmatrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{bmatrix}U^{T}$

注意：特征分解最右边的是特征矩阵的逆，只是拉普拉斯矩阵的性质才可以写成特征矩阵的转置。

2 傅里叶变换与其对Graph上的傅里叶变换的推广

2.1 图上的傅里叶变换

传统的傅里叶变换定义为：

$F(\omega)=\mathcal{F}[f(t)]=\int f(t) e^{-i \omega t} d t$

其本质是信号$f(x)$与基函数$e^{-i \omega t}$的积分。解释如下：

首先需要知道如下1和2的知识点：

1. 广义特征方程定义为：

$A V=\lambda V$

其中$A$是一种变换，$V$是特征向量或特征函数（无穷维向量），$\Lambda$是特征值。

2. $\Delta=\nabla^2=\underbrace{\nabla \bullet}_{散度}\underbrace{\nabla}_{梯度}$ 即：Laplace算子=n维欧几里德空间中的一个二阶微分算子= 梯度的散度 ：参考资料

则类比1和2，下式：
$\Delta e^{-i \omega t}=\frac{\partial^{2}}{\partial t^{2}} e^{-i \omega t}=-\omega^{2} e^{-i \omega t}$

中$e^{-i \omega t}$就是变换$\nabla$的特征函数，$\omega$(频率)和特征函数密切相关。

推广到图上，用到了拉普拉斯矩阵（即离散拉普拉斯算子），来寻找拉普拉斯矩阵的特征向量。

设$L$是拉普拉斯矩阵，$V$是特征向量，则：

$L V=\lambda V$

离散的积分就是内积，因此仿照上面定义图上的傅里叶变换：

$F\left(\lambda_{l}\right)=\hat{f}\left(\lambda_{l}\right)=\sum_{i=1}^{N} f(i) u_{l}^{*}(i)$

$f$是Graph上的 $N$ 维向量， $f(i)$ 与Graph的顶点一一对应， $u_l(i)$表示第 $l$ 个特征向量的第 $i$ 个分量。那么特征值（频率） $\lambda_l$ 下的， $f$ 的图傅里叶变换就是图上的每个节点与 $\lambda_l$ 对应的特征向量 $u_l$ 进行内积运算。

利用矩阵乘法将Graph上的傅里叶变换推广到矩阵形式：

$\left( \begin{array}{c}{\hat{f}\left(\lambda_{1}\right)} \\ {\hat{f}\left(\lambda_{2}\right)} \\ {\vdots} \\ {\hat{f}\left(\lambda_{N}\right)}\end{array}\right)=\left( \begin{array}{cccc}{u_{1}(1)} & {u_{1}(2)} & {\dots} & {u_{1}(N)} \\ {u_{2}(1)} & {u_{2}(2)} & {\dots} & {u_{2}(N)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {u_{N}(1)} & {u_{N}(2)} & {\dots} & {u_{N}(N)}\end{array}\right) \left( \begin{array}{c}{f(1)} \\ {f(2)} \\ {\vdots} \\ {f(N)}\end{array}\right)$

$f$在图上的傅里叶变换为：$\hat{f}=U^{T} f\qquad(a)$

2.2 图上的傅里叶逆变换

传统的傅里叶逆变换是对频率$\omega$求积分：

$\mathcal{F}^{-1}[F(\omega)]=\frac{1}{2 \Pi} \int F(\omega) e^{i \omega t} d \omega$

迁移到Graph上变为对特征值$\lambda_l$求和：

$f(i)=\sum_{l=1}^{N} \hat{f}\left(\lambda_{l}\right) u_{l}(i)$

利用矩阵乘法将Graph上的傅里叶逆变换推广到矩阵形式：

$\left( \begin{array}{c}{f(1)} \\ {f(2)} \\ {\vdots} \\ {f(N)}\end{array}\right)=\left( \begin{array}{cccc}{u_{1}(1)} & {u_{2}(1)} & {\dots} & {u_{N}(1)} \\ {u_{1}(2)} & {u_{2}(2)} & {\dots} & {u_{N}(2)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {u_{1}(N)} & {u_{2}(N)} & {\dots} & {u_{N}(N)}\end{array}\right) \left( \begin{array}{c}{\hat{f}\left(\lambda_{1}\right)} \\ {\hat{f}\left(\lambda_{2}\right)} \\ {\vdots} \\ {\hat{f}\left(\lambda_{N}\right)}\end{array}\right)$

即 $f$ 在图上傅里叶逆变换的矩阵形式为：$f=U \hat{f}\qquad(b)$

3 卷积

$(f * g)(t)=\int_{\mathbb{R}} f(x) g(t-x) d x$

详细请参考：

如何通俗地理解卷积？

离散卷积本质就是一种加权求和。CNN中的卷积本质上就是利用一个共享参数的过滤器（kernel），通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征的提取， 当然加权系数就是卷积核的权重系数。

那么卷积核的系数如何确定的呢？是随机化初值，然后根据误差函数通过反向传播梯度下降进行迭代优化。这是一个关键点，卷积核的参数通过优化求出才能实现特征提取的作用，GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。

4 卷积定理

卷积定理的百度解释，公式如下：

$f * g=\mathcal{F}^{-1}\{\mathcal{F}\{f\} \cdot \mathcal{F}\{g\}\}$

公式的意义：即一个域相乘，相当于另一个域卷积；一个域卷积，相当于另一个域相乘。图域卷积相当于傅立叶域相乘，那先对图和卷积核做傅立叶变换后相乘，再傅立叶反变换回来，就得到了图域卷积。

更多资料其参考：
Laplacian算子
参考资料之——图卷积网络(GCN)新手村完全指南

5 推广到图上

$f * h=\mathcal{F}^{-1}[\hat{f}(\omega) \hat{h}(\omega)]=\frac{1}{2 \Pi} \int \hat{f}(\omega) \hat{h}(\omega) e^{i \omega t} d \omega$

类比到图上并把傅里叶变换的定义带入， $f$ 与卷积核 $h$ 在Graph上的卷积可按下列步骤求出：

根据上文公式(a)，可得$f$的傅里叶变换为$\hat{f}=U^{T} f$

卷积核 $h$ 的傅里叶变换写成对角矩阵的形式即为：

$\left(\begin{array}{ccccc}{\hat{h}\left(\lambda_{1}\right)} & {} & {} & {} \\ {} & {\ddots} & {} \\ {} & {} & {\hat{h}\left(\lambda_{n}\right)}\end{array}\right)$

$\hat{h}\left(\lambda_{l}\right)=\sum_{i=1}^{N} h(i) u_{l}^{*}(i)$是根据需要设计的卷积核 $h$ （注意：这里自己设计的卷积和直接在频域设计，因此不需要傅里叶变换左乘矩阵$U$）在图上的傅里叶变换。

两者的傅立叶变换乘积即为：

$\left(\begin{array}{ccccc}{\hat{h}\left(\lambda_{1}\right)} & {} & {} & {} \\ {} & {\ddots} & {} \\ {} & {} & {\hat{h}\left(\lambda_{n}\right)}\end{array}\right) U^{T} f$

再乘以$U$求两者傅立叶变换乘积的逆变换，则求出卷积：

$(f * h)_{G}=U\left(\begin{array}{ccc}{\hat{h}\left(\lambda_{1}\right)} & {} & {} \\ {} & {\ddots} & {} \\ {} & {} & {\hat{h}\left(\lambda_{n}\right)}\end{array}\right) U^{T} f$

至此，上面这个公式对应原论文中公式(3)。

6 深度学习中的图卷积

图卷积的卷积核参数就是$\operatorname{diag}\left(\hat{h}\left(\lambda_{l}\right)\right)$

6.1 第一代图卷积

Spectral Networks and Locally Connected Networks on Graphs中简单粗暴地把$\operatorname{diag}\left(\hat{h}\left(\lambda_{l}\right)\right)$变成了卷积核$\operatorname{diag}\left(\theta_{l}\right)$，也就是：

$y_{\text {output}}=\sigma\left(U g_{\theta}(\Lambda) U^{T} x\right)\qquad(3)$

卷积核如下设计方式：

$g_{\theta}(\Lambda)=\left(\begin{array}{ccc}{\theta_{1}} \\ {} & {\ddots} & {} \\ {} & {} & {\theta_{n}}\end{array}\right)$

式（3）就是标准的第一代GCN中的层了，$\sigma(\cdot)$是激活函数，$\Theta=\left(\theta_{1}, \theta_{2}, \cdots, \theta_{n}\right)$是任意的参数，通过初始化赋值然后利用误差反向传播进行调整，$x$是图上上对应于每个顶点的特征向量（由特数据集提取特征构成的向量）。

第一代的参数方法存在着一些弊端：

• 每一次前向传播，都要计算$U, \operatorname{diag}\left(\theta_{l}\right)$和$U^{T}$三者的矩阵乘积，特别是对于大规模的图，计算的代价较高，也就是论文中的$\mathcal{O}\left(n^{2}\right)$计算复杂度。
• 卷积核需要 $n$ 个参数

6.2 第二代图卷积

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering（该篇论文推导特别清晰，可以仔细阅读阅读）把$\operatorname{diag}\left(\hat{h}\left(\lambda_{l}\right)\right)$巧妙的设计成$\sum_{j=0}^{K} \alpha_{j} \lambda_{l}^{j}$，即：

$y_{\text {output}}=\sigma\left(U g_{\theta}(\Lambda) U^{T} x\right)\qquad(4)$

$g_{\theta}(\Lambda)=\left(\begin{array}{ccc}{\sum_{j=0}^{K} \alpha_{j} \lambda_{1}^{j}} & {} \\ {} & {\ddots} & {} \\ {} & {} & {\sum_{j=0}^{K} \alpha_{j} \lambda_{n}^{j}}\end{array}\right)$

上面的公式仿佛还什么都看不出来，下面利用矩阵乘法进行变换，来一探究竟。

$\left(\begin{array}{ccc}{\sum_{j=0}^{K} \alpha_{j} \lambda_{1}^{j}} & {} \\ {} & {\ddots} & {} \\ {} & {} & {\sum_{j=0}^{K} \alpha_{j} \lambda_{n}^{j}}\end{array}\right)=\sum_{j=0}^{K} \alpha_{j} \Lambda^{j}$

进而可以导出：

$U \sum_{j=0}^{K} \alpha_{j} \Lambda^{j} U^{T}=\sum_{j=0}^{K} \alpha_{j} U \Lambda^{j} U^{T}=\sum_{j=0}^{K} \alpha_{j} L^{j}$

上式成立是因为$L^{2}=U \Lambda U^{T} U \Lambda U^{T}=U \Lambda^{2} U^{T}$ 且 $U^{T} U=E$

(4)式就变成了：

$y_{\text {output}}=\sigma\left(\sum_{j=0}^{K} \alpha_{j} L^{j} x\right)\qquad(5)$

其中 $\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{K}\right)$ 是任意的参数，通过初始化赋值然后利用误差反向传播进行调整。

式(5)所设计的卷积核其优点在于在于：

• 卷积核只有 $K$个参数，一般 $K$远小于 $n$，参数的复杂度被大大降低了。
• 矩阵变换后，神奇地发现不需要做特征分解了，直接用拉普拉斯矩阵$L$进行变换。然而由于要计算$L^j$，计算复杂度还是$\mathcal{O}\left(n^{2}\right)$（疑问）
• 卷积核具有很好的空间定位，并且$K$就是卷积核的感受野，也就是说每次卷积会将中心顶点$K$阶邻边上的点特征进行加权求和，$K=1$如下图：

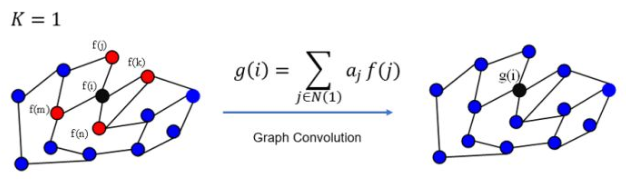
$K=2$如下图：

注：上图只是以一个顶点作为实例，GCN每一次卷积对所有的顶点都完成了图示的操作。

6.3 利用Chebyshev多项式递归计算卷积核

在第二代GCN中，$L$ 是 $n\times n$ 的矩阵，所以$L^j$的计算还是$\mathcal{O}\left(n^{2}\right)$ 复杂的， Wavelets on graphs via spectral graph theory提出了利用Chebyshev多项式拟合卷积核的方法，来降低计算复杂度。卷积核$g_{\theta}(\Lambda)$可以利用截断（truncated）的shifted Chebyshev多项式来逼近。

$g_{\theta}(\Lambda)=\sum_{k=0}^{K-1} \theta_{k}' T_{k}(\tilde{\Lambda})\qquad(6)$

$\theta_{k}'$是Chebyshev多项式的系数。至此，上式公式即为原论文中公式(4)

$T_{k}(\tilde{\Lambda})$是取$\tilde{\Lambda}=2 \Lambda / \lambda_{\max }-I$的Chebyshev多项式，进行这个shift变换的原因是：Chebyshev多项式的输入要在$[-1,1]$之间。

由Chebyshev多项式的性质，可以得到如下的递推公式：

$\begin{array}{l} T_{0}(\tilde{\Lambda})=I\\ T_{1}(\tilde{\Lambda})=\tilde{\Lambda}\\ T_{k}(\tilde{\Lambda}) =2 \tilde{\Lambda} T_{k-1}(\tilde{\Lambda}) -T_{k-2}(\tilde{\Lambda}) \qquad(7) \end{array}$

上式等式两边分别左乘$U$，右乘$U^T$，可得：

$\begin{array}{l} UT_{0}(\tilde{\Lambda})U^T=UIU^T=I=T_0(\tilde{L})\\ UT_{1}(\tilde{\Lambda})U^T=U\tilde{\Lambda}U^T=\tilde{L}=T_1(\tilde{L})\\ UT_{k}(\tilde{\Lambda}) U^T=U2 \tilde{\Lambda} T_{k-1}(\tilde{\Lambda}) U^T-UT_{k-2}(\tilde{\Lambda}) U^T\\ =U2 \tilde{\Lambda}U^TU T_{k-1}(\tilde{\Lambda}) U^T-UT_{k-2}(\tilde{\Lambda}) U^T\\ =2 \tilde{L} T_{k-1}(\tilde{L})-T_{k-2}(\tilde{L}) =T_k(\tilde{L}) \qquad(8) \end{array}$

其中$\tilde{L}=2 L / \lambda_{\max }-I$，则卷积运算如下：

$g_{\theta} \star x=U g_{\theta} U^{\top} x = U \sum_{k=0}^{K} \theta_{k}^{\prime} T_{k}(\tilde{\Lambda}) U^{\top} x = \sum_{k=0}^{K} \theta_{k}^{\prime} T_{k}(\tilde{L}) x\qquad(9)$

上式子就是原论文中的公式(5)。

我们注意到：

$T_{k}(\tilde{L}) x=2 \tilde{L} T_{k-1}(\tilde{L})x-T_{k-2}(\tilde{L})x\in R^n$

其中$x$是$n$维的由每个顶点的特征构成的向量当然，也可以是 $n\times m$ 的特征矩阵，这时每个顶点都有 $m$ 个特征，但是 $m$ 通常远小于 $n$

这个时候不难发现：式（9）的运算不再有矩阵乘积了，只需要计算矩阵与向量的乘积即可。计算一次$T_{k}(\tilde{L}) x$的复杂度是$\mathcal{O}(|E|)$，$E$是图中边的集合，则整个运算的复杂度是 $\mathcal{O}(K|E|)$ 。 当图是稀疏图($E\ll\frac{n(n-1)}{2}$)的时候，计算加速尤为明显，这个时候复杂度远低于 $\mathcal{O}\left(n^{2}\right)$

至此，原论文中公式(4)(5)以及算法简化的原因已解释清楚。

上面的讲述是GCN最基础的思路，很多论文中的GCN结构是在上述思路的基础上进行了一些简单数学变换。理解了上述内容，就可以做到“万变不离其宗”。

附录 傅里叶变换

1 什么是空间

注：本部分参考地址——欧几里得空间的数学结构

欧几里得空间$\mathbb{R}^n$是有序数组(称为点或向量) $(x_1,\ldots,x_n)$形成的集合，其中$x_i$为实数。在欧氏几何中，譬如平面几何与空间几何，我们可以计算两点之间的距离、多个向量的线性组合(向量加法与纯量乘法)、向量的长度，以及两个向量之间的夹角。

数学家将这些概念予以抽象化，并用公设化方式定义出不同的数学结构， 称为 空间。

在数学中，空间一词并不单独存在，我们可以称$X$是一个集合，但不讲$X$是一个空间。

粗浅地说，空间是一个赋予某种数学结构的集合，该数学结构决定空间的名称，

例如线性代数中大家熟悉的向量空间。

下面提到的欧氏空间$\mathbb{R}^n$的一些数学结构，背后的目的是将有限维空间延伸至无限维空间， 其中最重要的一个特例是希尔伯特(Hilbert)空间。

我了进一步了解空间，下面举几个常见空间的例子：

1.1 度量空间(Metric space)

度量空间(赋距空间，metric space)是一个集合(一般是非空集合)，并赋予一距离函数，称为度量(度规，metric)。具体而言，度量空间是一个二元组$(X,d)$，其中$X$为集合，度量$d:X\times X\to[0,\infty)$为非负函数，满足

(M1) $d(x,y)\ge 0$(非负性)
(M2) $d(x,y)=0\Leftrightarrow x=y$(不可区分者的同一性)
(M3) $d(x,y)=d(y,x)$(对称性)
(M4) $d(x,z)\le d(x,y)+d(y,z)$(三角不等式)

公理(M4)是欧几里得几何中三角不等式的抽象公式化，这是一个非常重要的定义性质。度量空间的四个公理并不独立，(M1) 可由其他三个公理推得：
$2d(x,y)=d(x,y)+d(y,x)\ge d(x,x)=0。$
给定集合$X$，度量$d$有许多合法的定义。例如，考虑$X=\mathbb{R}^n$的两点$x=(x_1,\ldots,x_n)$和$y=(y_1,\ldots,y_n)$，欧氏距离
$\displaystyle d_2(x,y)=\left(\sum_{i=1}^n(x_i-y_i)^2\right)^{1/2}$
或曼哈顿距离(Manhattan distance)
$\displaystyle d_1(x,y)=\sum_{i=1}^n\vert x_i-y_i\vert$
皆为集合$X$上的度量(有兴趣可自行验证$d_2$和$d_1$满足上述公理)。因此，即便$(X,d_2)$和$(X,d_1)$有相同的底层集(underlying set) $X$，两者是不同的度量空间。事实上，给定一个非空集合$X$，存在无限多个度量空间。譬如，若$d$是定义于$X$的一个度量，则$d_\alpha(x,y)=\alpha d(x,y)，\alpha>0$，也是在$X$上的度量。

1.2 向量空间(Vector space)

向量空间(vector space)，或称线性空间(linear space)，是一种代数结构，核心概念在于线性组合(合并向量加法与纯量乘法)。我们称$\mathcal{V}$是一个布于体(域，field) $F$的向量空间，若$\mathbf{x},\mathbf{y}\in\mathcal{V}$与$\alpha\in F$具备向量加法$\mathbf{x}+\mathbf{y}$和纯量乘法$\alpha\mathbf{x}$，并满足下列公理：

(V1) $\mathbf{x}+\mathbf{y}=\mathbf{y}+\mathbf{x}$(交换律)
(V2) $\mathbf{x}+(\mathbf{y}+\mathbf{z})=(\mathbf{x}+\mathbf{y})+\mathbf{z}$(结合律)
(V3)存在唯一的$\mathbf{0}\in\mathcal{V}$使得$\mathbf{x}+\mathbf{0}=\mathbf{x}$
(V4)存在唯一的$-\mathbf{x}\in\mathcal{V}$使得$\mathbf{x}+(-\mathbf{x})=\mathbf{0}$
(V5) $\alpha(\beta\mathbf{x})=(\alpha\beta)\mathbf{x}$(结合律)
(V6) $1\mathbf{x}=\mathbf{x}$
(V7) $\alpha(\mathbf{x}+\mathbf{y})=\alpha\mathbf{x}+\alpha\mathbf{y}$(分配律)
(V8) $(\alpha+\beta)\mathbf{x}=\alpha\mathbf{x}+\beta\mathbf{x}$(分配律)

• 若$F=\mathbb{R}$，则$\mathcal{V}$称为实向量空间；
• 若$F=\mathbb{C}$，则$\mathcal{V}$称为复向量空间。
• 在线性代数中，欧氏空间$\mathbb{R}^n$是最常见的一个向量空间， 其中的元素$(x_1,\ldots,x_n)$构造一个$n$维实向量$\mathbf{x}$。
• 线性映射(变换)则是向量空间中最重要的运算机制。设$\mathcal{V}$和$\mathcal{W}$为布于相同数系的向量空间，我们称$T:\mathcal{V}\to\mathcal{W}$为一个线性映射，若任意$\mathbf{x},\mathbf{y}\in\mathcal{V}$和纯量$\alpha$满足
  $\displaystyle\begin{aligned} T(\mathbf{x}+\mathbf{y})&=T(\mathbf{x})+T(\mathbf{y})\\ T(\alpha\mathbf{x })&=\alpha T(\mathbf{x}).\end{aligned}$
  线性映射出现在许多科学与工程领域， 这是我们对向量空间如此重视的原因。

1.2.1 线性代数的代数结构

注：本部分参考资料地址——线性代数里的代数结构

阿贝尔群（可交换群）

实例1：

纯量加法的代数结构是阿贝尔群
考虑整数集$\mathbb{Z}$(包含正整数、负整数与零)，我们观察出任两个整数的加法运算满足以下五个性质：

• 加法具有封闭性，如果$x$和$y$属于$\mathbb{Z}$，那么$x+y$也属于$\mathbb{Z}$。

• 加法具有交换性，两整数之和与其计算位置无关，
  $x+y=y+x$。

• 加法具有结合性，排序固定的三个整数之和与其执行加法的顺序无关，
  $(x+y)+z=x+(y+z)$。

• 存在一整数$0$使得任何整数与其相加皆不改变，
  $x+0=0+x=x$，

  因此$0$也称为加法单位元。

• 任何加法都可以「回复」，意即每一整数皆存在逆元，如下：
  $x+(-x)=(-x)+x=0$。

实例2：

考虑正实数集$\mathbb{R}_{+}$，并以$\times$表示一般的乘法运算：
$x\times y=xy$。

明显地，正实数乘法满足封闭性、交换性与结合性。上例中$0$的角色被实数$1$所取代，$1$称为乘法单位元，满足下式：

$x\times 1=1\times x=x$。

每一个正实数$x$的逆元为其倒数，因为

$\displaystyle x\times\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)\times x=1$。

结论

上例整数$\mathbb{Z}$的加法$+$与正实数$\mathbb{R}_{+}$的乘法$\times$共同满足的五个性质即为阿贝尔群的定义。

正式定义： 给定一个集合${G}$与二元运算$\ast$，若满足上述五个性质，即封闭性、交换性、结合性，存在一运算单位元，且每一元素皆存在对应的逆元，我们便称$({G},\ast)$为阿贝尔群。

不可交换群

如果二元运算$\ast$除交换性外，满足其余四个性质， 则称为不可交换群或简称群。

不难验证$(\mathbb{R},+)$是一个群(也是阿贝尔群)，但$(\mathbb{R},\times)$不构成一个群，因为$0$不存在逆元，亦即不存在$x$使得$0x=1$。若将$0$剔除， 令$\mathbb{R}^{\ast}=\mathbb{R}\!\setminus\!\{0\}$，则$(\mathbb{R}^{\ast},\times)$为一个阿贝尔群。 明显地，若将实数$\mathbb{R}$扩大为复数$\mathbb{C}$，以上陈述仍然成立。

体（域）

从有理数$\mathbb{Q}$，实数$\mathbb{R}$和复数$\mathbb{C}$的性质如何归纳出体的定义呢？上述三种数系都具备加法与乘法运算：

• 对$+$而言，$\mathbb{Q}$、$\mathbb{R}$，$\mathbb{C}$是阿贝尔群；
• 对$\times$而言，$\mathbb{Q}^{\ast}$，$\mathbb{R}^{\ast}$，$\mathbb{C}^{\ast}$(排除$0$所得的集合)也都是阿贝尔群；
• 剩下的工作只要再将这两种运算联系在一起，此即分配律：

$\begin{aligned} \alpha (x+y)=\alpha x+\alpha y \\ (\alpha+\beta)x=\alpha x+\beta x \end{aligned}$

因此，我们归纳出体（域）的定义：一个体$\mathbb{F}$是一个集合并赋予$+$和$\times$ 运算，而且$(\mathbb{F},+)$和$(\mathbb{F}^{\ast},\times)$皆为阿贝尔群并满足分配律。

向量空间的定义

（如何理解布于一个体？）

布于一个体$\mathbb{F}$(其中元素称为纯量)的一个向量空间$(\mathcal{V},+,\cdot)$(其中元素称为向量)是一个加法阿贝尔群（即$(\mathcal{V},+)$是一个阿贝尔群），并赋予纯量$\alpha$与向量$\mathbf{x}$的乘法运算，简称为纯量乘法，其结果$\alpha\cdot\mathbf{x}$为属于$(\mathcal{V},+,\cdot)$的一个向量。以下向量空间记为$\mathcal{V}$，并省略乘法符号$\cdot$。为了使纯量乘法运算适当地配合既有的三种运算$( \mathbb{F}$的加法，$\mathcal{V}$的加法，$\mathbb{F}$的乘法)，还必须满足下列四个性质：

向量分配律：对于$\alpha,\beta\in{F}，\mathbf{x}\in\mathcal{V}，(\alpha+\beta)\mathbf{x}=\alpha\mathbf{x}+\beta\mathbf{x}。$
纯量分配律：对于$\alpha\in{F}，\mathbf{x},\mathbf{y}\in\mathcal{V}，\alpha(\mathbf{x}+\mathbf{y})=\alpha\mathbf{x}+\alpha\mathbf{y}。$
结合律：对于$\alpha,\beta\in{F}，\mathbf{x}\in\mathcal{V}，(\alpha\beta)\mathbf{x}=\alpha(\beta\mathbf{x})。$
纯量单位元：对于$\mathbf{x}\in\mathcal{V}，存在1\in\mathbb{F}，使得1\mathbf{x}=\mathbf{x}。$

我们惊奇的发现：阿贝尔群$(\mathcal{V},+)$所满足的最后四个性质（扣除封闭性），再加上前述四个纯量乘法性质正是向量空间所必须满足的八个公理！

1.3 赋范向量空间(Normed vector space)

定义于度量空间的连续映射与定义于向量空间的线性映射可以合成为一个连续线性映射，具体的作法是将距离与长度引进向量空间，这个概念称为范数(norm)。对于一个布于体$F$的向量空间$\mathcal{V}$，实函数$\Vert\mathbf{x}\Vert$称为范数，其中$\mathbf{x}\in\mathcal{V}$，若下列性质成立：

(N1) $\Vert\mathbf{x}\Vert\ge 0，\Vert\mathbf{x}\Vert=0 \Leftrightarrow\mathbf{x}=\mathbf{0}$(非负性)
(N2) $\Vert\alpha\mathbf{x}\Vert=\vert\alpha\vert\cdot\Vert\mathbf{x}\Vert，\alpha\in F$是任一纯量(均匀性)
(N3) $\Vert\mathbf{x}+\mathbf{y}\Vert\le\Vert\mathbf{x}\Vert+\Vert\mathbf{y}\Vert$(三角不等式)

一个赋范向量空间(normed vector space)是二元组($\mathcal{V},\Vert\cdot\Vert$)，其中$\mathcal{V}$是一个向量空间，$\Vert\cdot\Vert$是定义于$\mathcal{V}$的一个范数。赋范向量空间($\mathcal{V},\Vert\cdot\Vert$)是一个度量空间：给定任意$\mathbf{x},\mathbf{y}\in\mathcal{V}$，
$\displaystyle d(\mathbf{x},\mathbf{y})=\Vert\mathbf{x}-\mathbf{y}\Vert$
是定义于$\mathcal{V}$的一个度量。(N1)表明$\Vert\mathbf{x}-\mathbf{y}\Vert\ge 0$，且$\Vert\mathbf{x}-\mathbf{y}\Vert=0$等价于$\mathbf{x}=\mathbf{y}$，故满足(M1)与(M2)。设$\alpha=-1$，由(N2)可得$\Vert-(\mathbf{x}-\mathbf{y})\Vert=\Vert\mathbf{x}-\mathbf{y}\Vert$，满足(M3)。最后，由(N3)可得
$\displaystyle \Vert\mathbf{x}-\mathbf{y}\Vert=\Vert\mathbf{x}-\mathbf{z}+\mathbf{z}-\mathbf{y}\Vert\le\Vert\mathbf{x}-\mathbf{z}\Vert+\Vert\mathbf{z}-\mathbf{y}\Vert，$
此即(M4) 的三角不等式。

1.4 内积空间(Inner product space)

我们已经将欧氏几何中两点之间的距离、向量的线性组合，以及向量的长度等概念抽象化，最后剩下两向量之间的夹角，与此相关的概念是内积(inner product)和正交(orthogonality)。令$\mathcal{V}$为复向量空间。内积是一个映射$\mathcal{V}\times\mathcal{V}\to\mathbb{C}$，记为$\left\langle\mathbf{x},\mathbf{y}\right\rangle，其中\mathbf{x},\mathbf{y}\in\mathcal{V}$，并满足下列公理

(I1) $\left\langle\mathbf{x},\mathbf{x}\right\rangle\ge 0，\left\langle\mathbf{x},\mathbf{x}\right\rangle=0\Leftrightarrow\mathbf{x}=\mathbf{0}$(非负性)
(I2) $\left\langle\mathbf{x},\mathbf{y}+\mathbf{z}\right\rangle=\left\langle\mathbf{x},\mathbf{y}\right\rangle+\left\langle\mathbf{x},\mathbf{z}\right\rangle$(可加性)
(I3) $\left\langle\mathbf{x},\alpha\mathbf{y}\right\rangle=\alpha\left\langle\mathbf{x},\mathbf{y}\right\rangle$(均匀性)
(I4) $\left\langle\mathbf{x},\mathbf{y}\right\rangle=\overline{\left\langle\mathbf{y},\mathbf{x}\right\rangle}$(共轭对称性)

内积空间(inner product space)是一个二元组$(\mathcal{V},\left\langle\cdot,\cdot\right\rangle)$，其中$\mathcal{V}$是向量空间，$\left\langle\cdot,\cdot\right\rangle$是定义于$\mathcal{V}$的内积。若$\left\langle\mathbf{x},\mathbf{y}\right\rangle=0$，我们说向量$\mathbf{x}$和$\mathbf{y}$是正交的。正交是内积空间中最重要的一个概念，正交使得内积空间拥有完善的几何性质，例如正交投影。内积空间$(\mathcal{V},\left\langle\cdot,\cdot\right\rangle)$是一个赋范向量空间。我们可以证明

$\displaystyle \Vert\mathbf{x}\Vert=\left\langle\mathbf{x},\mathbf{x}\right\rangle^{1/2}$

是一个范数。不难证明$\Vert\mathbf{x}\Vert$满足(N1)和(N2)。下面证明(N3)三角不等式成立。写出

$\displaystyle\begin{aligned} \Vert\mathbf{x}+\mathbf{y}\Vert^2&=\left\langle\mathbf{x}+\mathbf{y},\mathbf{x}+\mathbf{y}\right\rangle=\Vert\mathbf{x}\Vert^2+\left\langle\mathbf{x},\mathbf{y}\right\rangle+\left\langle\mathbf{y},\mathbf {x}\right\rangle+\Vert\mathbf{y}\Vert^2\\ &=\Vert\mathbf{x}\Vert^2+2Re(\left\langle\mathbf{x} ,\mathbf{y}\right\rangle)+\Vert\mathbf{y}\Vert^2\le\Vert\mathbf{x}\Vert^2+2\vert\left\langle\mathbf{x},\mathbf{y}\right\rangle\vert+\Vert\mathbf{y}\Vert^2. \end{aligned}$

使用Schwarz不等式$\vert\left\langle\mathbf{x},\mathbf{y}\right\rangle\vert\le\Vert\mathbf{x}\Vert\cdot\Vert\mathbf{y}\Vert$，可得

$\displaystyle \Vert\mathbf{x}+\mathbf{y}\Vert^2\le\Vert\mathbf{x}\Vert^2+2\Vert\mathbf{x}\Vert\cdot\Vert\mathbf{ y}\Vert+\Vert\mathbf{y}\Vert^2=(\Vert\mathbf{x}\Vert+\Vert\mathbf{y}\Vert)^2。$

如果一内积空间是完备度量空间，则称之为希尔伯特空间(即完备内积空间)。 因此，希尔伯特空间是定义了内积的巴拿赫空间。

1.5 总结

最后我用一张图呈现欧氏空间$\mathbb{R}^n$的数学结构阶层关系，$X$空间$\to Y$空间表示$X$空间蕴含$Y$空间，各空间的核心概念总结于下：

度量空间：度量(距离)
向量空间：线性组合
赋范向量空间：范数(长度)
巴拿赫空间：范数与完备性
内积空间：内积(角度)
希尔伯特空间：内积与完备性

2 函数空间

注：本部分参考地址——从几何空间到函数空间

基础线性代数课程常将讨论的向量空间局限于有限维几何向量空间$\mathbb{R}^n$，下文通过问答方式，介绍如何将几何向量空间延伸推广至函数空间。

Q1：如果将$n$维实向量空间$\mathbb{R}^n$扩展至无限维实向量空间$\mathbb{R}^{\infty}$，此空间需满足何种条件始有利于实际应用？

A：很明显，$\mathbb{R}^{\infty}$里的向量$\mathbf{v}$包含无限多个元，如
$\mathbf{v}=\begin{bmatrix} v_1\\ v_2\\ v_3\\ \vdots \end{bmatrix}。$
如果我们不对向量的元$v_i$加入限制，那么此空间将过于庞大，反而令我们无所适从。对$v_i$设限的最简单方式是透过向量$\mathbf{v}$的长度，我们只对那些有限长度的向量感到兴趣，同时也希望几何向量空间的向量长度定义在此依然适用，亦即
$\Vert\mathbf{v}\Vert^2=v_1^2+v_2^2+v_3^2+\cdots$
这个无穷级数必须收敛至一有限数值，例如，无限维空间包含向量$(1,\frac{1}{2},\frac{1}{3}$,$\cdots)^T$，但不含$(1,1,1,\cdots)^T$。

加入了有限向量长度的限制，此无限维空间仍符合向量空间的定义吗？是的。有限长度向量$\mathbf{x}$与$\mathbf{y}$之和其长度还是有限的，因为
$\Vert\mathbf{x}+\mathbf{y}\Vert\le\Vert\mathbf{x}\Vert+\Vert\mathbf{y}\Vert，$
而且纯量乘积$a\mathbf{x}$的长度也是有限的。很容易验证向量空间的八个向量加法和纯量乘法性质依然成立，我们称之为希尔伯特(Hilbert)空间， 即一个保有一般几何性质的无限维实向量空间。希尔伯特空间也具有正交性质，我们说向量$\mathbf{x}$和$\mathbf{y}$是正交的，若其内积为零：
$\mathbf{x}^T\mathbf{y}=x_1y_1+x_2y_2+x_3y_3+\cdots=0。$
当然，歌西—舒瓦兹(Cauchy-Schwarz) 不等式也成立：
$\vert\mathbf{x}^T\mathbf{y}\vert\le\Vert\mathbf{x}\Vert \Vert\mathbf{y}\Vert。$

Q2：希尔伯特空间与函数空间有什么关系？函数空间又该如何定义向量内积？

A：不需要受过专业数学训练，业余人士也可以看穿希尔伯特空间的外表伪装。用一个例子说明，考虑定义于区间$0\le x\le 2\pi$的正弦函数$f(x)=\sin x$，我们将函数$f$当作一个无限维向量，向量的各元即为连续区间内的函数值$\sin x$。当向量的元是连续时，前述向量长度定义已不适用，各元平方和应该改为积分，如下：
$\begin{aligned} \Vert f\Vert^2&=\displaystyle\int_{0}^{2\pi}(f(x))^2dx=\int_{0}^{2\pi}(\sin x )^2dx=\pi\end{aligned}。$
此算式的意义重大，我们确实可以量测函数的长度，等于指出函数也是向量， 而仅包含有限长度的函数可以形成向量空间，因此希尔伯特空间变成了一个函数空间(function space)。

若$f(x)=\sin x，g(x)=\cos x$，运用同样的想法，将数列之和替换为积分可以产生两个函数的内积。

以$\langle f,g\rangle$表示函数$f$和$g$的内积，例如：
$\begin{aligned} \langle f,g\rangle&=\displaystyle\int_{0}^{2\pi}f(x)g(x)dx=\int_{0}^{2\pi}\sin x \cos x dx=0\end{aligned}，$
可知$\sin x$与$\cos x$正交。函数的长度可由内积求得，$\Vert f\Vert^2=\langle f,f\rangle$，舒瓦兹不等式则表示为$\vert\langle f,g\rangle\vert\le\Vert f\Vert \Vert g\Vert$。

Q3：能否举个实用的函数空间例子，它包含哪些基底函数，如何产生座标？

A：最有名的例子是傅立叶级数(Fourier series)，函数$f(x)$表示为正弦函数和余弦函数的展开式：
$f(x)=a_0+a_1\cos x+b_1\sin x+a_2\cos 2x+b_2\sin 2x+\cdots$
傅立叶级数的基底函数包含
$1, \cos x, \sin x, \cos 2x, \sin 2x,\cdots$
傅立叶级数的系数即为参考此基底的座标，如要计算$a_1$，可于等号两端同乘$\cos x$，再从$0$积分至$2\pi$：
$\begin{aligned} \displaystyle\int_{0}^{2\pi}f(x)\cos x dx&=a_0\int_0^{2\pi}\cos x dx+a_1\int_0^{2\pi} (\cos x)^2 dx\\ &+b_1\int_0^{2\pi}\sin x\cos x dx+a_2\int_0^{2\pi}\cos 2x\cos x dx+b_2\int_0^ {2\pi}\sin 2x\cos x dx+\cdots\end{aligned}$
等号右边除了对应系数$a_1$的项，其余所有项皆为零，有兴趣可自行验证正弦函数与余弦函数互为正交。因此，$a_1$可由下式得到
$\begin{aligned} a_1&=\displaystyle\frac{\int_0^{2\pi}f(x)\cos x dx}{\int_{0}^{2\pi}(\cos x)^2 dx} =\frac{\langle f,\cos x\rangle}{\langle\cos x,\cos x\rangle}\end{aligned}。$
其他系数也可以使用同样方式求得，如欲计算$b_1$，将$\cos x$改为$\sin x$，又如欲计算$a_2$，则将$\cos x$改为$\cos 2x$。

傅立叶级数的应用相当广泛：

• 一方面因为傅立叶选择了一组正交基底函数，$f(x)$的系数很容易得到
• 另一方面这组由正弦与余弦构成的基底能将问题转移至等价且适合发展理论分析的空间

---

至此，已完成了空间承上启下的讲解：

• 呈上：完成了上次报告没有解释的空间的定义
• 启下：引出了本次报告需要讲解的傅里叶变换的基础：傅里叶级数

---

3 从傅立叶级数到傅立叶变换

后文参考资料包含以下链接：

如何通俗地理解傅立叶变换？
如何理解傅立叶级数公式？
从傅立叶级数到傅立叶变换
如何理解拉普拉斯变换？

3.1 傅立叶级数

让·巴普蒂斯·约瑟夫·傅立叶男爵（1768 －1830）猜测任意周期函数都可以写成三角函数之和。比如下面这个周期为$2\pi$的方波，可以用大量的正弦波的叠加来逼近：

3.1.1 傅立叶级数是向量

从代数上看，傅立叶级数就是通过三角函数和常数项来叠加逼近周期为$T$的函数$f(x)$：

$\displaystyle f(x)=a_0+\sum _^{\infty}\left(a_{n}cos({\frac{2\pi n}{T}x})+b_{n}sin({\frac{2\pi n}{T}x})\right),a_0\in\mathbb{R}$

实际上是把$f(x)$当作了如下基的向量：
$\{1,cos({\frac{2\pi n}{T}x}),sin({\frac{2\pi n}{T}x})\}$
那么上面的式子就可以解读为：
$\displaystyle f(x)=\underbrace{a_0}_{基1下的坐标}\cdot 1+\sum _^{\infty }\left(\underbrace{a_{n}}_{对应基的坐标}cos({\frac{2\pi n}{T}x})+\underbrace{b_{n}}_{对应基的坐标}sin({\frac{2\pi n}{T}x})\right)$
说具体点，比如刚才提到的，$T=2\pi$的方波$f(x)$，可以初略的写作：
$f(x)\approx 1+\frac{4}{\pi}sin(x)$
从几何上看，有那么一丁点相似：

我们可以认为：
$f(x)\approx 1+\frac{4}{\pi}sin(x)$
此函数的基为：
$\{1,sin(x)\}$
则$f(x)$相当于向量：
$\displaystyle (1,\frac{4}{\pi})$
画到图上如下，注意坐标轴不是$x,y$，而是$1,sin(x)$：

3.1.2 频域图

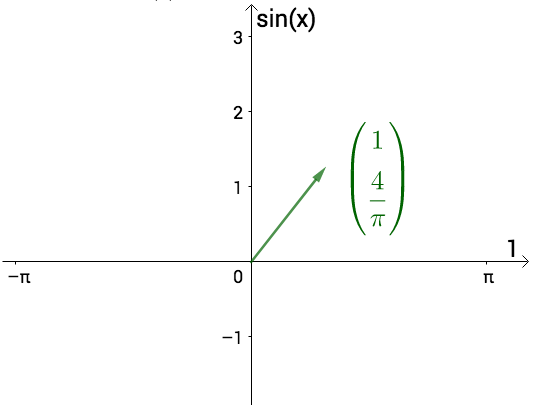
再增加几个三角函数：
$$f(x)\approx 1+\frac{4}{\pi}sin(x)+0sin(2x)+\frac{4}{3\pi}sin(3x)+0sin(4x)+\frac{4}{5\pi}sin(5x)$4
从几何上看，肯定更接近了：

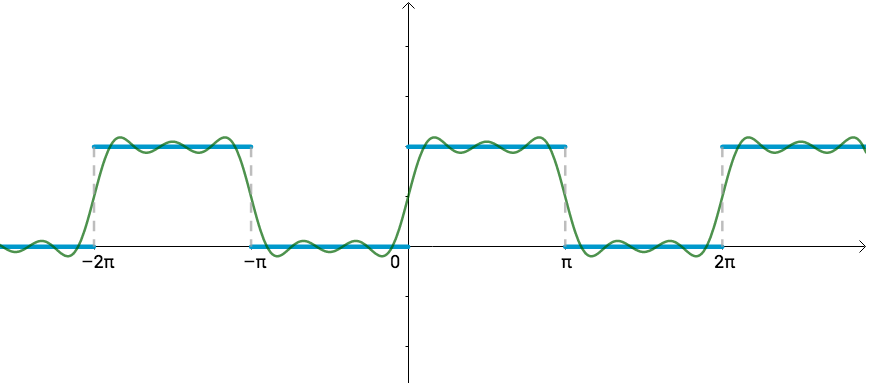
此时基为：
$\{1,sin(x),sin(2x),sin(3x),sin(4x),sin(5x)\}$
对应的向量为：
$\displaystyle (1,\frac{4}{\pi},0,\frac{4}{3\pi},0,\frac{4}{5\pi})$
六维的向量没有办法画图啊，没关系，数学家发明了一个频域图来表示这个向量：

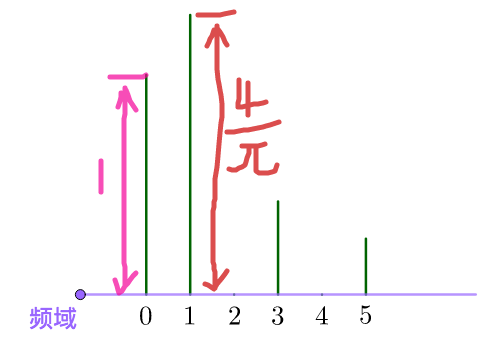
上图中的$0,1,2,3,4,5$分别代表了不同频率的正弦波函数，也就是之前的基：
$0Hz\iff sin(0x)\quad 3Hz\iff sin(3x)\cdots$
而高度则代表在这个频率上的振幅，也就是这个基上的坐标分量。
这里举的例子只有正弦函数，余弦函数其实也需要这样一个频谱图，也就是需要两个频谱图。
原来的曲线图就称为时域图，往往把时域图和频域图画在一起，这样能较为完整的反映傅立叶级数：

不管时域、频域其实反映的都是同一个曲线，只是一个是用函数的观点，一个是用向量的观点。
当习惯了频域之后，会发现看到频域图，似乎就看到了傅立叶级数的展开：

3.2 非周期函数

非周期函数，比如下面这个函数可以写出傅立叶级数吗？

这并非一个周期函数，没有办法写出傅立叶级数。
不过可以变换一下思维，如果刚才的方波的周期：
$T=2\pi\to T=\infty$
那么就得到了这个函数：

在这样的思路下，就可以使用三角级数来逼近这个函数：

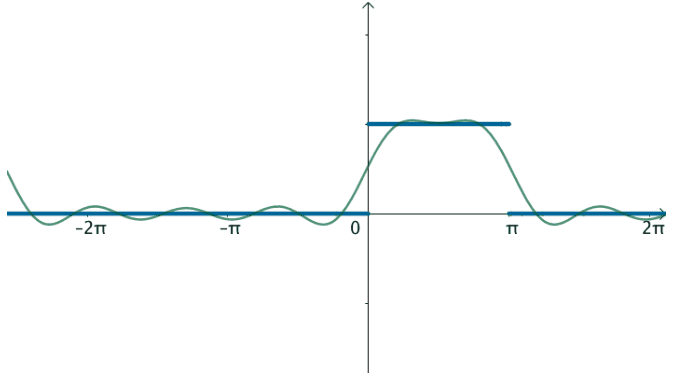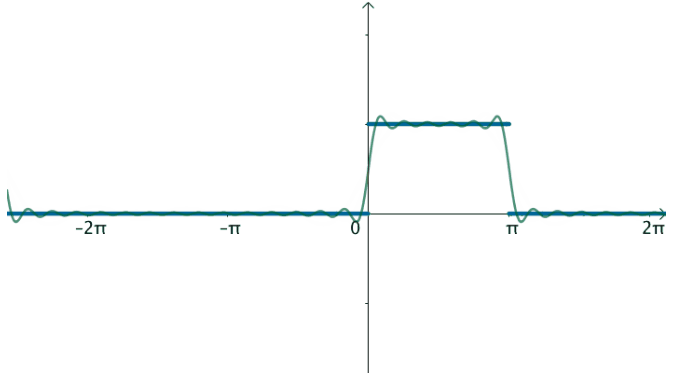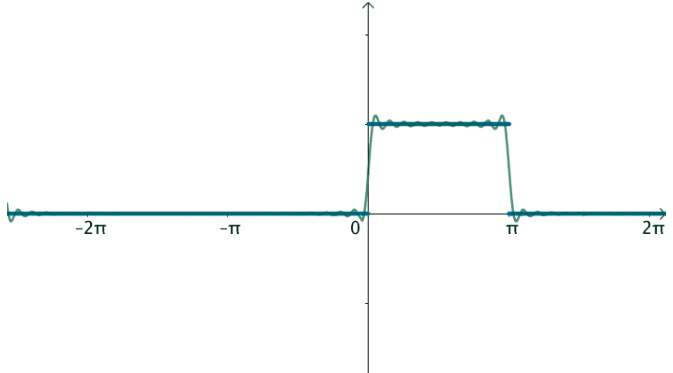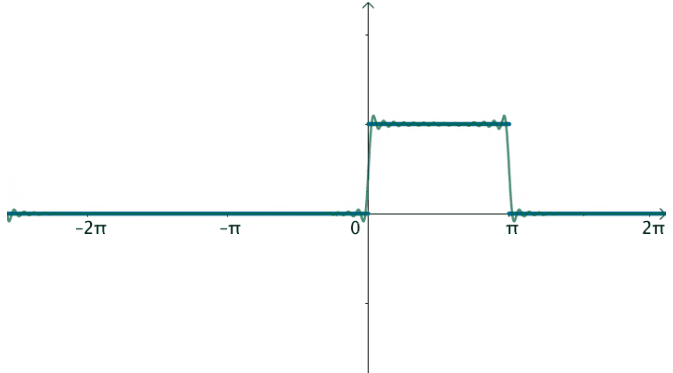
观察下频域，之前说了，对于周期为$T$的函数$f(x)$，其基为：
$\{1,cos({\frac{2\pi n}{T}x}),sin({\frac{2\pi n}{T}x})\}$
刚才举的方波$T=2\pi$，对应的基就为（没有余弦波）：
$\{1,sin(x),sin(2x),sin(3x),sin(4x),sin(5x),\cdots\,sin(nx)\}$
对应的频率就是：
$\{0Hz,1Hz,2Hz,3Hz,4Hz,5Hz,\cdots\,nHz\}$
按照刚才的思路，如果$T$不断变大，比如让$T=4\pi$，对应的基就为（没有余弦波）：
$\{1,sin(0.5x),sin(x),sin(1.5x),sin(2x),sin(2.5x),\cdots\,sin(0.5nx)\}$
对应的频率就是：
$\{0Hz,0.5Hz,1Hz,1.5Hz,2Hz,2.5Hz,\cdots\,0.5nHz\}$
和刚才相比，频率更加密集：

之前的方波的频域图，画了前50个频率，可以看到，随着T不断变大，这50个频率越来越集中：

可以想象，如果真的：
$T=2\pi\to T=\infty$
这些频率就会变得稠密，直至连续，变为一条频域曲线：

傅立叶变换就是，让$T=\infty$，求出上面这根频域曲线。

3.3 傅立叶变换

之前说了，傅立叶级数是：

$\displaystyle f(x)=a_0+\sum _^{\infty}\left(a_{n}cos({\frac{2\pi n}{T}x})+b_{n}sin({\frac{2\pi n}{T}x})\right),a_0\in\mathbb{R}$

这里有正弦波，也有余弦波，画频域图也不方便，通过欧拉公式，可以修改为复数形式：

$f(x)=\sum _^{\infty }c_{n}\cdot e^{i\frac{2\pi nx}{T}}$

其中：
$\displaystyle c_{n}={\frac{1}{T}}\int _{x_0}^{x_0+T}f(x)\cdot e^{i\frac{2\pi nx}{T}}dx$
复数形式也是向量，可以如下解读：

$\displaystyle f(x)=\sum _^{\infty}\underbrace{c_{n}}_{对应基的坐标}\cdot \underbrace{e^{i\frac{2\pi nx}{T}}}_{正交基}$

不过$c_{n}$是复数，不好画频域图，所以之前讲解全部采取的是三角级数。
周期推向无穷的时候可以得到：

$\begin{array}{r}{f(x)=\sum_{n=-\infty}^{\infty} c_{n} \cdot e^{i \frac{2 \pi n x}{T}}} \\ {T=\infty}\end{array} \} \Longrightarrow f(x)=\int_{-\infty}^{\infty} F(\omega) e^{i \omega x} d \omega$

上面简化了一下，用$\omega$代表频率。

$F(\omega)$大致是这么得到的：
$\begin{array}{r}{c_{n}=\frac{1}{T} \int_{x_{0}}^{x_{0}+T} f(x) \cdot e^{-i \frac{2 \pi n x}{T}} d x} \\ {T=\infty}\end{array} \} \Rightarrow F(\omega)= \int_{-\infty}^{\infty} f(x) e^{-i \omega x} d x$

$F(\omega)$就是傅立叶变换，得到的就是频域曲线。
下面两者称为傅立叶变换对，可以相互转换：

$f(x)\iff F(\omega)$

结论：看待同一个数学对象的两种形式，一个是函数，一个是向量。